Curso de Análisis Exploratorio de Datos
Published:
¿Qué es el análisis exploratorio de datos?
- Proceso de conocer en detalle a tus datos, darles sentido.
- Determinar como tratar a los datos.
- Interrogarlos para obtener las respuestas que necesites.
- Transformarlos en información útil.
¿Cómo hacer un análisis exploratorio de datos?
Por que debería hacer un análisis exploratorio de datos?:
- Organizar y entender las variables: podrás identificar los diferentes tipos de variables, las categorías a la que pertenecen y el tipo de análisis que puedes realizar sobre ellas.
- Establecer relaciones entre las variables
- Encontrar patrones ocultos en los datos: podrás encontrar información o comportamientos relevantes cuando hagas el EDA.
- Ayuda a escoger el modelo correcto para la necesidad correcta: una vez encuentres como están relacionadas las variables podrás descubrir las variables que mas se ajustan a un tipo de modelo y de esta manera eligiras el correcto
- Ayuda a tomar decisiones informadas: decisiones basadas en los datos, en las relaciones que encuentres entre variables, en patrones ocultos y en los modelos que generes a través de la EDA
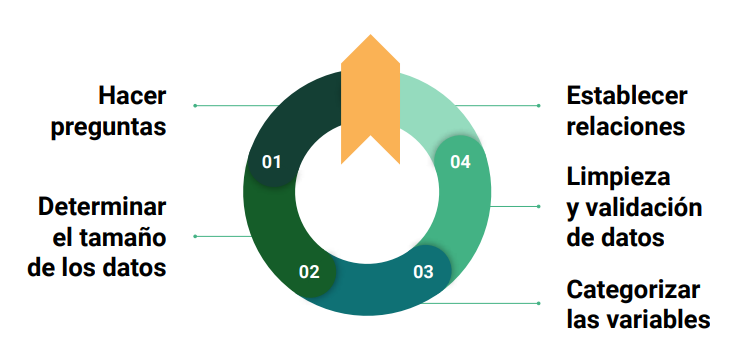
Pasos de una Análisis Exploratorio de Datos:
- Hacer preguntas sobe los datos. Hazte las siguientes preguntas para guiar el EDA:
- Que te gustaria encontrar?
- Que quisieras saber de los datos?
- Cual es la razon para realizar el analisis?
- Determinar el tamaño de los datos. Debes responder preguntas como:
- Cuantas observaciones existen?
- Cuantas variables hay?
- Necesito todas las observaciones?
- Necesito todas las variables?
- Categorizar las variables. Debes preguntarte:
- Cuantas variables categóricas existen?
- Cuantas variables continuas existen?
- Como puedo explorar cada variable dependiendo de su categoría?
- Limpieza y validación de los datos. En ese paso debes preguntarte:
- Tengo valores faltantes?
- Cual es la proporción de datos faltantes?
- Como puedo tratar a los datos faltantes?
- Cual es la distribución de los datos?
- Tengo valores atipicos?
- Establecer relaciones entre los datos. Responde preguntas como:
- Existe algun tipo de relacion entre mi variable X y Y?
- Que pasa ahora si considero la variable Z en el analisis?
- Que significa que las observaciones se agrupen?
- Que significa el patron que se observa?
Este proceso es ciclico. A pesar de que pueda parecer infinito, este proceso en algun momento debe salir del ciclo y continuar para obtener algun tipo de valor
En algún momento debes romperlo y continuar
Tipos de analítica de datos
- Descriptiva: ¿Qué sucedió? Provee de ideas sobre eventos del pasado.
- Prescriptiva: ¿Qué podría pasar si? Profundiza para encontrar las causas del evento.
- Predictiva: ¿Por qué sucedió? Utiliza los datos del pasado para predecir un futuro evento.
- Diagnóstica: ¿Qué debería hacerse? Analiza decisiones y eventos del pasado para estimar la probabilidad de diferentes resultados.
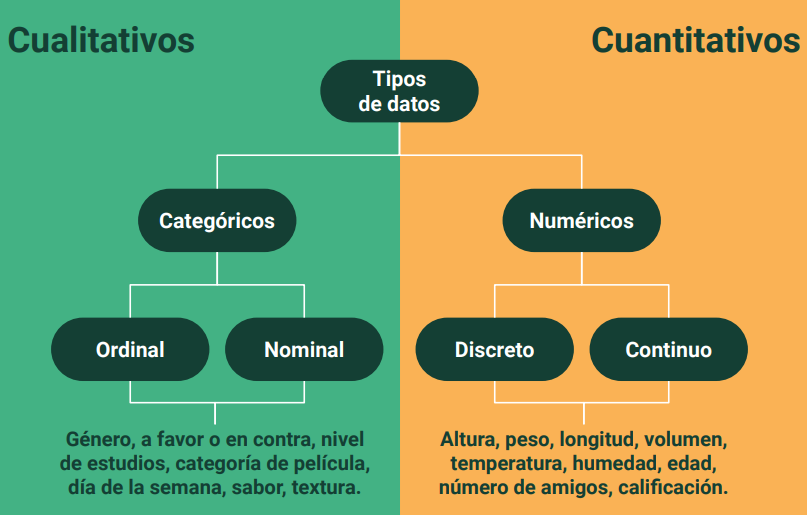
Tipos de datos y análisis de variables
Análisis de Datos
- Análisis Univariado
Analizar cada variable por separado. - Análisis Bivariado
Analizar la relación de cada par de variables. - Análisis Multivariado
Analizar el efecto simultáneo de múltiples variables.
Herramientas de software para el análisis exploratorio de datos

Conociendo nuestros datos: palmerpenguins
La base de datos Palmer Penguins es un conjunto de datos que contiene información sobre tres especies de pingüinos en las Islas Shetland del Sur, en la Antártida. Fue creada como una alternativa a la famosa base de datos Iris y se utiliza comúnmente para enseñar análisis de datos y técnicas de visualización.
Características Principales:
- Especies de Pingüinos: Incluye datos sobre tres especies: Adélie, Chinstrap y Gentoo.
- Variables: Contiene variables como el sexo, el tamaño del cuerpo (longitud del pico, longitud de la aleta, etc.), y el peso.
- Objetivo: Facilitar el aprendizaje de métodos estadísticos y de visualización de datos, así como fomentar la conservación de especies.
Link para conocer más sobre la base de datos https://pallter.marine.rutgers.edu/. Para descargar la información https://raw.githubusercontent.com/allisonhorst/palmerpenguins/master/inst/extdata/penguins.csv.
Principales bibliotecas empleadas
import matplotlib.pyplot as plt
import numpy as np
# from palmerpenguins.penguins import load_penguins
import palmerpenguins
import pandas as pd
from scipy import stats
import seaborn as sns
from sklearn import metrics
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.stats as ss
import empiricaldist
penguin_color = {
'Adelie': '#ff6602ff',
'Gentoo': '#0f7175ff',
'Chinstrap': '#c65dc9ff'
}
Recolección de datos, limpieza y validación
Primaria
Datos recolectados de primera mano a través de encuestas, entrevistas, experimentos y otros.Secundaria
Datos previamente recolectados por una fuente primaria externa al usuario primario. Por ejemplo, datos de departamentos de gobierno o empresas similares a la del usuario primario.Terciaria
Son datos que se adquieren de fuentes completamente externas al usuario primario. Por ejemplo, a través de proveedores de datos.
Validación de datos
- El proceso de asegurar la consistencia y precisión dentro de un conjunto de datos. https://www.safe.com/what-is/data-validation/
- Si los datos no son precisos desde el comienzo, los resultados definitivamente no serán precisos. https://www.safe.com/what-is/data-validation/
¿Qué se debe validar para asegurar consistencia?
- Modelo de datos.
- Seguimiento de formato estándar de archivos.
- Tipos de datos.
- Rango de variables.
- Unicidad.
- Consistencia de expresiones.
- Valores nulos.
## Datos Crudos
# raw_penguins_df = palmerpenguins.load_penguins_raw()
# raw_penguins_df
## Datos previamente procesados
# preprocessed_penguins_df = palmerpenguins.load_penguins()
# preprocessed_penguins_df
## Datos de Seaborn
preprocessed_penguins_df = sns.load_dataset("penguins")
Podemos importar la información desde un archivo empleando Pandas
## Datos crudos
raw_penguins_df2 = pd.read_csv('data/penguins_raw.csv')
## datos previamente procesados
preprocessed_penguins_df2 = pd.read_csv('data/penguins.csv')
Ejercicio de validación de datos
¿Qué tipo de dato son las variables del conjunto de datos?
## Trabajaremos con estos datos
preprocessed_penguins_df = pd.read_csv('data/penguins.csv')
preprocessed_penguins_df.dtypes
species object
island object
bill_length_mm float64
bill_depth_mm float64
flipper_length_mm float64
body_mass_g float64
sex object
year int64
dtype: object
¿Cuántas variables de cada tipo de dato tenemos en el conjunto de datos?
(
preprocessed_penguins_df
.dtypes
.value_counts()
)
float64 4
object 3
int64 1
Name: count, dtype: int64
¿Cuántas variables y observaciones tenemos en el conjunto de datos?
preprocessed_penguins_df.shape
(344, 8)
¿Existen valores nulos explicitos en el conjunto de datos?
(
preprocessed_penguins_df
.isnull()
.any()
)
species False
island False
bill_length_mm True
bill_depth_mm True
flipper_length_mm True
body_mass_g True
sex True
year False
dtype: bool
De tener observaciones con valores nulos, ¿cuántas tenemos por cada variable?
(
preprocessed_penguins_df
.isna()
.sum()
.sort_values(ascending=False)
)
sex 11
bill_length_mm 2
bill_depth_mm 2
flipper_length_mm 2
body_mass_g 2
species 0
island 0
year 0
dtype: int64
(
preprocessed_penguins_df
.isnull()
.sum()
.sort_values(ascending=False)
)
sex 11
bill_length_mm 2
bill_depth_mm 2
flipper_length_mm 2
body_mass_g 2
species 0
island 0
year 0
dtype: int64
En Pandas, isna() e isnull() son funciones que sirven para identificar valores nulos en un DataFrame o una Serie. Sin embargo, ambas funciones son prácticamente equivalentes y se pueden usar indistintamente. Aquí te explico brevemente sus características:
isna()
- Descripción: Identifica los valores nulos (NaN) en un DataFrame o una Serie.
- Uso:
dataframe.isna()
isnull()
- Descripción: También identifica los valores nulos (NaN) en un DataFrame o una Serie.
- Uso:
dataframe.isnull()
Diferencias
- Sinónimos: No hay diferencia funcional entre ambas; son sinónimos.
- Preferencia: La elección de uno sobre el otro es cuestión de estilo personal o de preferencia en el código.
¿Cuántos valores nulos tenemos en total en el conjunto de datos?
(
preprocessed_penguins_df
.isnull()
.sum()
.sum()
)
19
¿Cuál es la proporción de valores nulos por cada variable?
.melt(value_name='missing'): Transforma el DataFrame de formato ancho a formato largo, creando dos columnas: una para las variables originales y otra (missing) que indica si hay un valor nulo (True o False).
multiple='fill': Permite que las barras se apilen mostrando la proporción de valores nulos frente a valores no nulos.
(
preprocessed_penguins_df
.isnull()
.melt(value_name='missing')
.pipe(
lambda df: (
sns.displot(
data=df,
y='variable',
hue='missing',
multiple='fill',
aspect=2
)
)
)
)
plt.show()
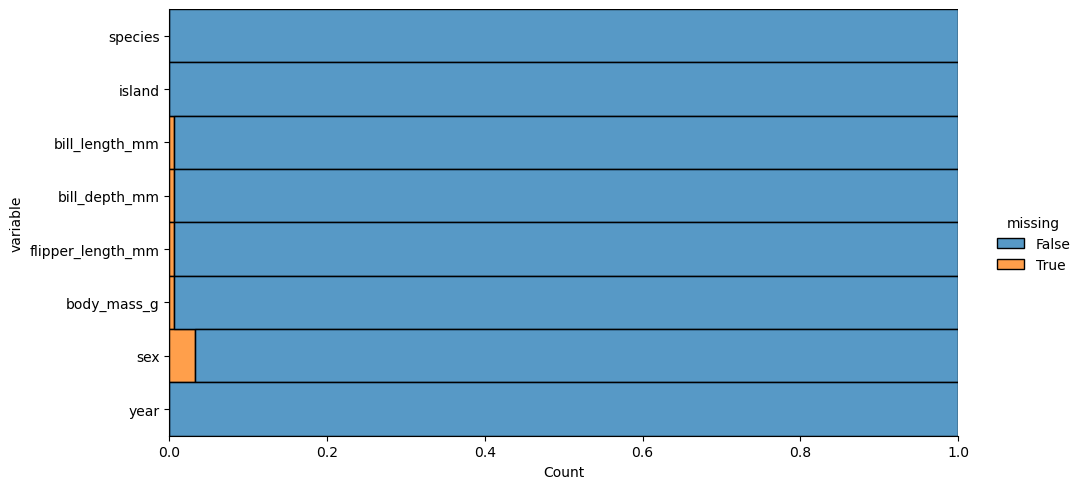
¿Cómo podemos visualizar los valores nulos en todo el conjunto de datos?
Puede suceder que todos estos valores nulos sean de un solo sujeto (fila) del dataset.
(
preprocessed_penguins_df
.isnull()
.transpose()
.pipe(
lambda df: sns.heatmap(data=df)
)
)
plt.show()
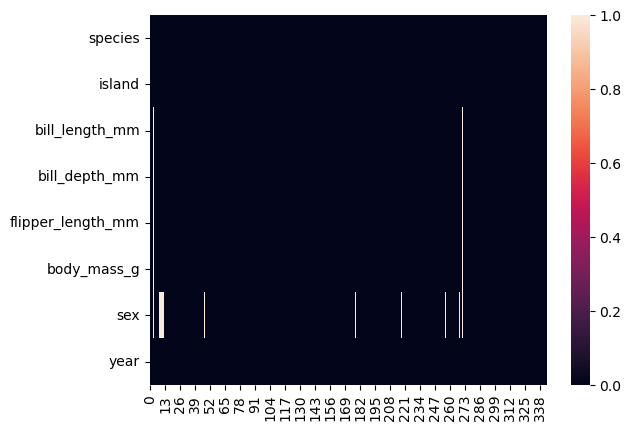
No todos los valores nulos son de un solo sujeto, observamos que el dato del sexo es el que presenta mayor cantidad de datos nulos.
¿Cuántas observaciones perdemos si eliminamos los datos faltantes?
processed_penguins_df = (
preprocessed_penguins_df
.dropna()
)
processed_penguins_df.shape, preprocessed_penguins_df.shape
((333, 8), (344, 8))
Observamos que tenemos 11 filas menos.
Análisis univariado
Conteos y proporciones
- Tabulación: Contabiliza la frecuencia de aparición de cada valor único de una variable.
- Proporciones: Relación de correspondencia entre las partes y el todo.
Extendiendo la idea de conteo mediante tabulación cruzada o tablas de contingencia.
Todas las variables
processed_penguins_df.describe(include='all')
| species | island | bill_length_mm | bill_depth_mm | flipper_length_mm | body_mass_g | sex | year | |
|---|---|---|---|---|---|---|---|---|
| count | 333 | 333 | 333.000000 | 333.000000 | 333.000000 | 333.000000 | 333 | 333.000000 |
| unique | 3 | 3 | NaN | NaN | NaN | NaN | 2 | NaN |
| top | Adelie | Biscoe | NaN | NaN | NaN | NaN | male | NaN |
| freq | 146 | 163 | NaN | NaN | NaN | NaN | 168 | NaN |
| mean | NaN | NaN | 43.992793 | 17.164865 | 200.966967 | 4207.057057 | NaN | 2008.042042 |
| std | NaN | NaN | 5.468668 | 1.969235 | 14.015765 | 805.215802 | NaN | 0.812944 |
| min | NaN | NaN | 32.100000 | 13.100000 | 172.000000 | 2700.000000 | NaN | 2007.000000 |
| 25% | NaN | NaN | 39.500000 | 15.600000 | 190.000000 | 3550.000000 | NaN | 2007.000000 |
| 50% | NaN | NaN | 44.500000 | 17.300000 | 197.000000 | 4050.000000 | NaN | 2008.000000 |
| 75% | NaN | NaN | 48.600000 | 18.700000 | 213.000000 | 4775.000000 | NaN | 2009.000000 |
| max | NaN | NaN | 59.600000 | 21.500000 | 231.000000 | 6300.000000 | NaN | 2009.000000 |
Solo las numéricas
processed_penguins_df.describe(include=[np.number])
| bill_length_mm | bill_depth_mm | flipper_length_mm | body_mass_g | year | |
|---|---|---|---|---|---|
| count | 333.000000 | 333.000000 | 333.000000 | 333.000000 | 333.000000 |
| mean | 43.992793 | 17.164865 | 200.966967 | 4207.057057 | 2008.042042 |
| std | 5.468668 | 1.969235 | 14.015765 | 805.215802 | 0.812944 |
| min | 32.100000 | 13.100000 | 172.000000 | 2700.000000 | 2007.000000 |
| 25% | 39.500000 | 15.600000 | 190.000000 | 3550.000000 | 2007.000000 |
| 50% | 44.500000 | 17.300000 | 197.000000 | 4050.000000 | 2008.000000 |
| 75% | 48.600000 | 18.700000 | 213.000000 | 4775.000000 | 2009.000000 |
| max | 59.600000 | 21.500000 | 231.000000 | 6300.000000 | 2009.000000 |
Solo categóricas - 1
processed_penguins_df.describe(include=object)
| species | island | sex | |
|---|---|---|---|
| count | 333 | 333 | 333 |
| unique | 3 | 3 | 2 |
| top | Adelie | Biscoe | male |
| freq | 146 | 163 | 168 |
Solo categóricas - 2
(
processed_penguins_df
.astype(
{
'species': 'category',
'island': 'category',
'sex': 'category'
}
)
.describe(include=['category', object])
)
| species | island | sex | |
|---|---|---|---|
| count | 333 | 333 | 333 |
| unique | 3 | 3 | 2 |
| top | Adelie | Biscoe | male |
| freq | 146 | 163 | 168 |
processed_penguins_df.describe()
| bill_length_mm | bill_depth_mm | flipper_length_mm | body_mass_g | year | |
|---|---|---|---|---|---|
| count | 333.000000 | 333.000000 | 333.000000 | 333.000000 | 333.000000 |
| mean | 43.992793 | 17.164865 | 200.966967 | 4207.057057 | 2008.042042 |
| std | 5.468668 | 1.969235 | 14.015765 | 805.215802 | 0.812944 |
| min | 32.100000 | 13.100000 | 172.000000 | 2700.000000 | 2007.000000 |
| 25% | 39.500000 | 15.600000 | 190.000000 | 3550.000000 | 2007.000000 |
| 50% | 44.500000 | 17.300000 | 197.000000 | 4050.000000 | 2008.000000 |
| 75% | 48.600000 | 18.700000 | 213.000000 | 4775.000000 | 2009.000000 |
| max | 59.600000 | 21.500000 | 231.000000 | 6300.000000 | 2009.000000 |
¿Cómo visualizar los conteos?
(
processed_penguins_df
.species
.value_counts()
.plot(
kind='bar',
color=penguin_color.values()
)
)
plt.show()
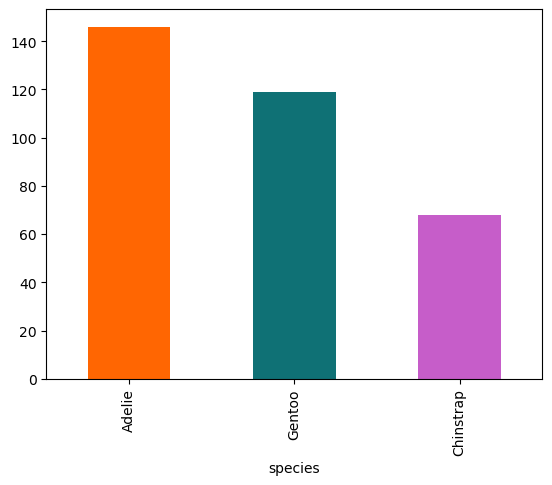
Seaborn
sns.catplot(
data=processed_penguins_df,
x='species',
kind='count',
hue='species',
palette=penguin_color,
# order=processed_penguins_df.value_counts('species', sort=True).index
)
plt.show()
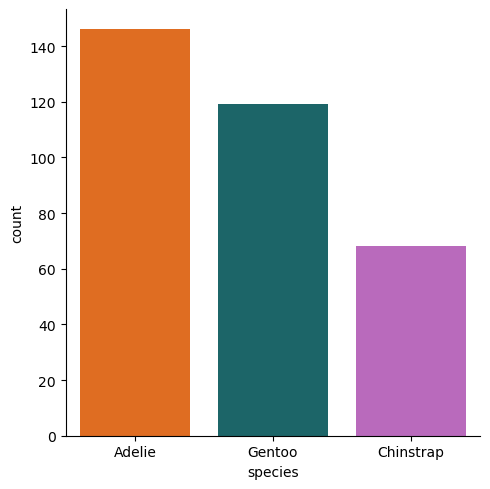
Ahora hacemos que Seaborn cuente por nosotros.
(
processed_penguins_df
.value_counts('species', sort=True) # Valores por especies ordenados
.reset_index(name='count') # Reiniciar el índice
.pipe(
lambda df: (
sns.barplot(
data=df,
x='species',
y='count',
hue='species',
palette=penguin_color
)
)
)
)
plt.show()
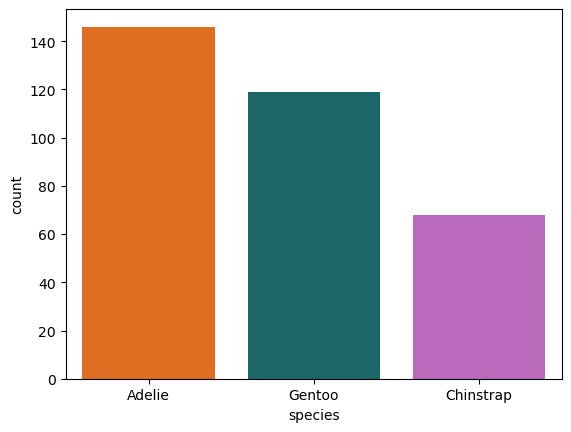
¿Cómo visualizar las proporciones?
Con respecto al Curso de Platzi hay un cambio de .add_column('x', '') por .assign=(x='').
(
processed_penguins_df
.assign(x='')
.pipe(
lambda df: (
sns.displot(
data=df,
x='x',
hue='species',
multiple='fill',
palette=penguin_color
)
)
)
)
plt.show()
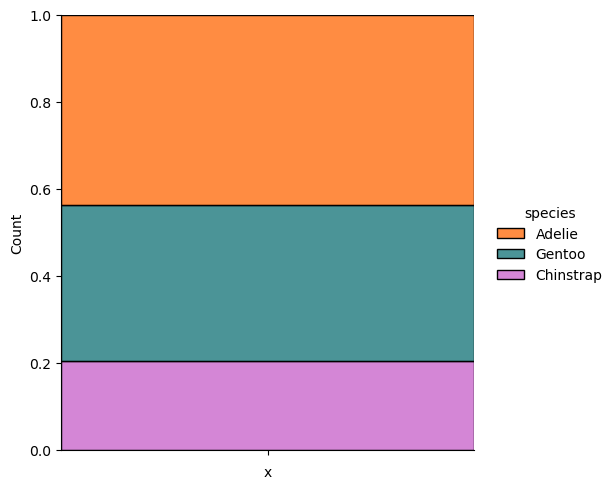
# Convert relevant columns to 'category' dtype
processed_penguins_df = processed_penguins_df.astype({
'species': 'category',
'island': 'category',
'sex': 'category'
})
category_cols = processed_penguins_df.select_dtypes('category').columns
fig, axs = plt.subplots(1, len(category_cols), figsize=(15, 5))
for i in range(len(category_cols)):
(
processed_penguins_df
.value_counts(category_cols[i], sort=True)
.reset_index(name='count')
.pipe(
lambda df:(
sns.barplot(
ax=axs[i],
data=df,
x=category_cols[i],
y='count',
)
)
)
)
plt.show()
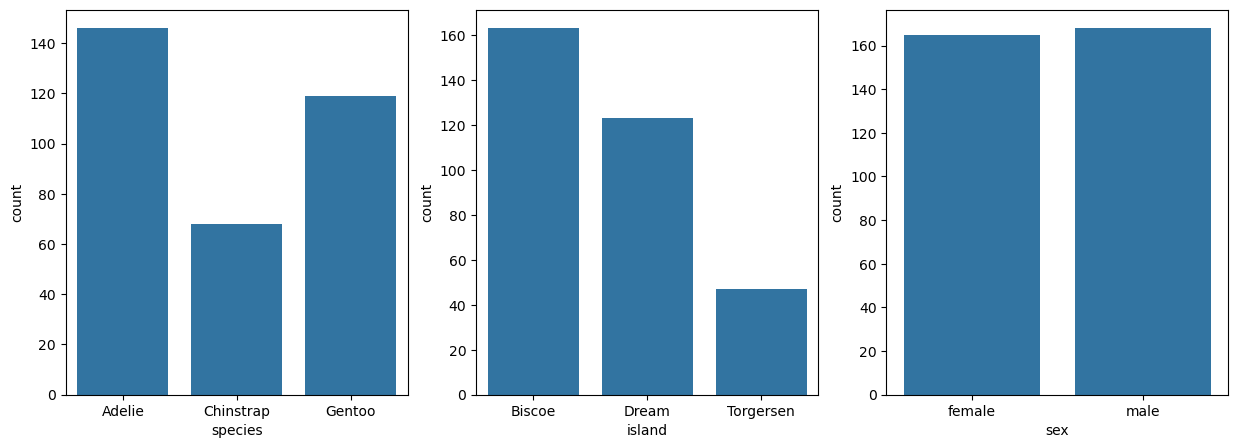
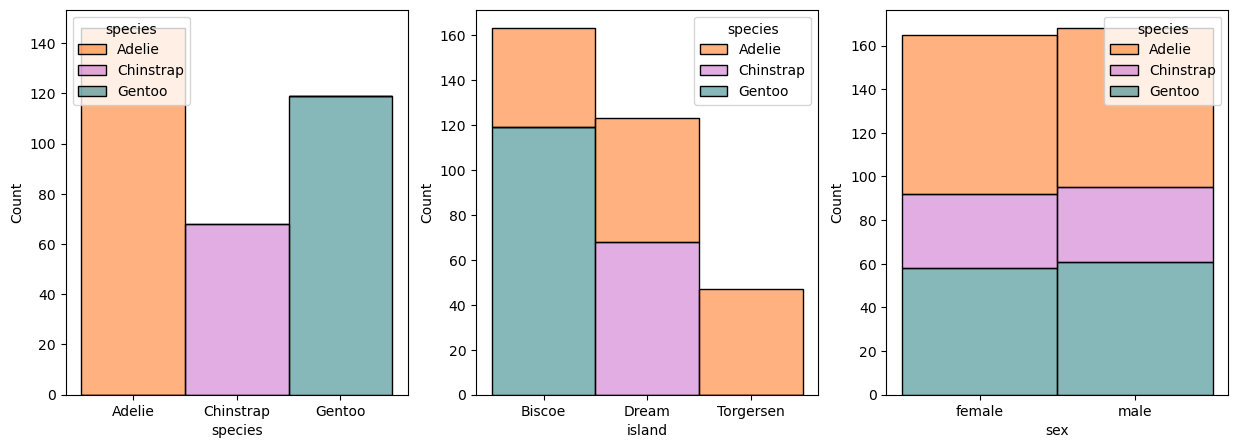
fig,ax = plt.subplots(1,3,figsize=(15,5))
for i in range(len(category_cols)):
sns.histplot(
ax=ax[i],
data=processed_penguins_df,
x=category_cols[i],
hue='species',
multiple='stack',
palette=penguin_color,
alpha=0.5
)
plt.show()
Medidas de tendencia central
- Media (promedio).
- Mediana (dato central).
- Moda (dato que más se repite).
- Media ponderada.
- Media armónica.
- Media geométrica.
Media o promedio
processed_penguins_df = (
preprocessed_penguins_df
.dropna()
)
processed_penguins_df.bill_depth_mm.mean(), np.mean(processed_penguins_df.bill_depth_mm)
(17.164864864864867, 17.164864864864867)
processed_penguins_df.mean(numeric_only=True)
bill_length_mm 43.992793
bill_depth_mm 17.164865
flipper_length_mm 200.966967
body_mass_g 4207.057057
year 2008.042042
dtype: float64
processed_penguins_df.median(numeric_only=True)
bill_length_mm 44.5
bill_depth_mm 17.3
flipper_length_mm 197.0
body_mass_g 4050.0
year 2008.0
dtype: float64
processed_penguins_df.mode()
| species | island | bill_length_mm | bill_depth_mm | flipper_length_mm | body_mass_g | sex | year | |
|---|---|---|---|---|---|---|---|---|
| 0 | Adelie | Biscoe | 41.1 | 17.0 | 190.0 | 3800.0 | male | 2009 |
processed_penguins_df.describe(include=object)
| species | island | sex | |
|---|---|---|---|
| count | 333 | 333 | 333 |
| unique | 3 | 3 | 2 |
| top | Adelie | Biscoe | male |
| freq | 146 | 163 | 168 |
Medidas de dispersión
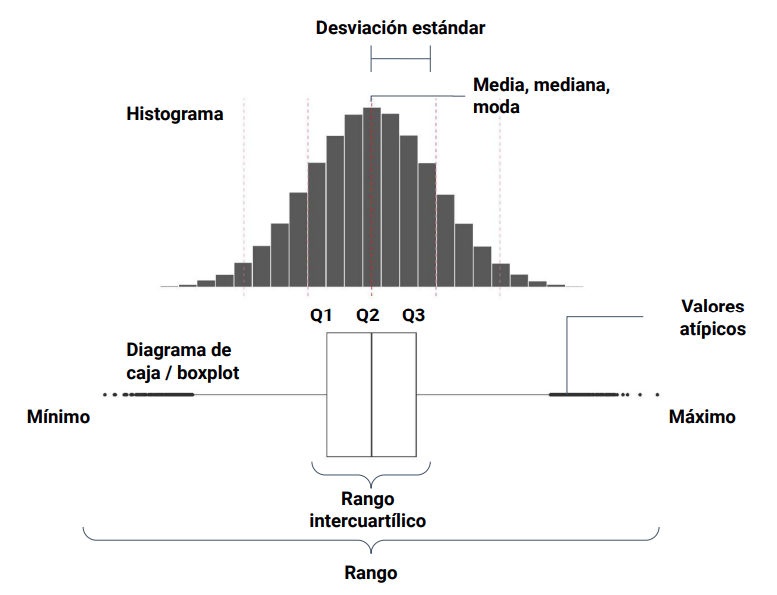
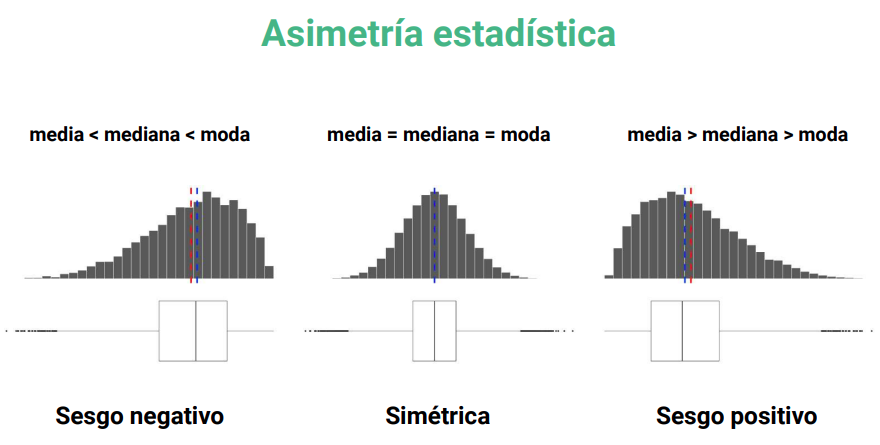
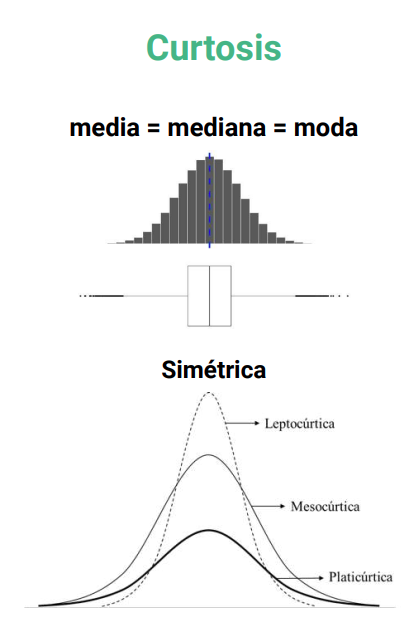
¿Cuál es el valor máximo de las variables?
processed_penguins_df.max(numeric_only=True)
bill_length_mm 59.6
bill_depth_mm 21.5
flipper_length_mm 231.0
body_mass_g 6300.0
year 2009.0
dtype: float64
¿Cuál es el valor mínimo de las variables?
processed_penguins_df.min(numeric_only=True)
bill_length_mm 32.1
bill_depth_mm 13.1
flipper_length_mm 172.0
body_mass_g 2700.0
year 2007.0
dtype: float64
¿Cuál es el rango de las variables?
processed_penguins_df.max(numeric_only=True) - processed_penguins_df.min(numeric_only=True)
bill_length_mm 27.5
bill_depth_mm 8.4
flipper_length_mm 59.0
body_mass_g 3600.0
year 2.0
dtype: float64
¿Cuál es la desviación estándar de las variables?
processed_penguins_df.std(numeric_only=True)
bill_length_mm 5.468668
bill_depth_mm 1.969235
flipper_length_mm 14.015765
body_mass_g 805.215802
year 0.812944
dtype: float64
¿Cuál es el rango intercuartílico?
processed_penguins_df.quantile(0.25, numeric_only=True)
bill_length_mm 39.5
bill_depth_mm 15.6
flipper_length_mm 190.0
body_mass_g 3550.0
year 2007.0
Name: 0.25, dtype: float64
processed_penguins_df.quantile(0.75,numeric_only=True) - \
processed_penguins_df.quantile(0.25,numeric_only=True)
bill_length_mm 9.1
bill_depth_mm 3.1
flipper_length_mm 23.0
body_mass_g 1225.0
year 2.0
dtype: float64
(
processed_penguins_df
.quantile(q=[0.75, 0.50, 0.25], numeric_only=True)
.transpose()
.rename_axis('metric')
.reset_index()
.assign( # Add el rango intercuartilico
iqr = lambda df: df[0.75] - df[0.25]
)
)
| metric | 0.75 | 0.5 | 0.25 | iqr | |
|---|---|---|---|---|---|
| 0 | bill_length_mm | 48.6 | 44.5 | 39.5 | 9.1 |
| 1 | bill_depth_mm | 18.7 | 17.3 | 15.6 | 3.1 |
| 2 | flipper_length_mm | 213.0 | 197.0 | 190.0 | 23.0 |
| 3 | body_mass_g | 4775.0 | 4050.0 | 3550.0 | 1225.0 |
| 4 | year | 2009.0 | 2008.0 | 2007.0 | 2.0 |
¿Cómo puedo visualizar la distribución de una variable?
Histograma
sns.histplot(
data=processed_penguins_df,
x='flipper_length_mm',
)
plt.axvline(
x=processed_penguins_df.flipper_length_mm.mean(),
color='red',
linestyle='dashed',
linewidth=2,
label='mean'
)
plt.axvline(
x=processed_penguins_df.flipper_length_mm.median(),
color='blue',
linestyle='dashed',
linewidth=2,
label='median'
)
plt.axvline(
x=processed_penguins_df.flipper_length_mm.mode().values[0],
color='black',
linestyle='dashed',
linewidth=4,
label='mode'
)
plt.axvline(
x=processed_penguins_df.flipper_length_mm.quantile(0.25),
color='yellow',
linestyle='dashed',
linewidth=2,
label='Q1'
)
plt.axvline(
x=processed_penguins_df.flipper_length_mm.quantile(0.75),
color='green',
linestyle='dashed',
linewidth=2,
label='Q3'
)
plt.legend()
plt.show()
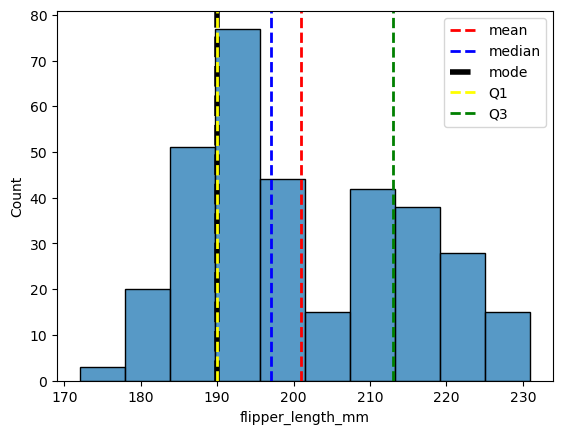
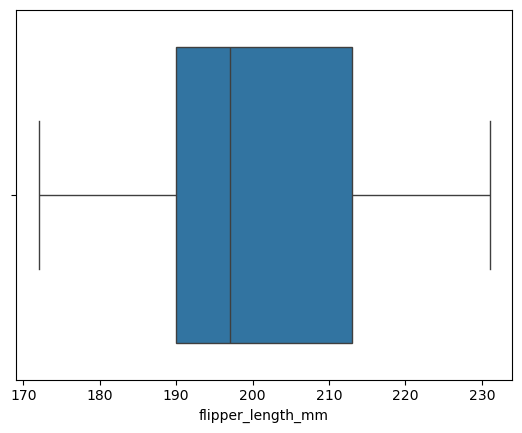
Diagrama de caja / boxplot
sns.boxplot(
x=processed_penguins_df.flipper_length_mm,
)
plt.show()
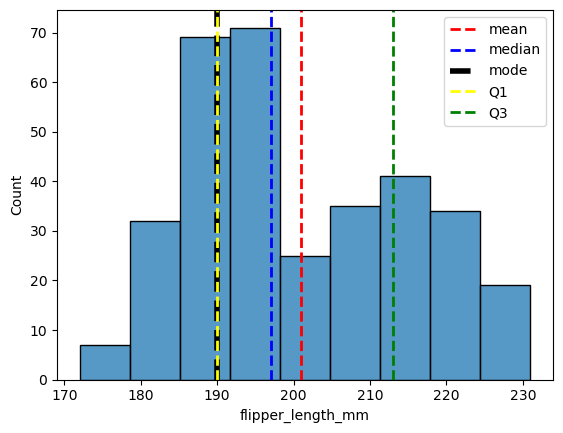
Limitaciones
def freedman_diaconis_bindwidth(x: pd.Series) -> float:
"""Find optimal bindwidth using Freedman-Diaconis rule."""
IQR = x.quantile(0.75) - x.quantile(0.25)
N = x.size
return 2 * IQR / N ** (1 / 3)
print(f"Optimal bindwidth " +
f"{freedman_diaconis_bindwidth(processed_penguins_df.flipper_length_mm)}")
Optimal bindwidth 6.636560948202412
sns.histplot(
data=processed_penguins_df,
x='flipper_length_mm',
binwidth=6.3
)
plt.axvline(
x=processed_penguins_df.flipper_length_mm.mean(),
color='red',
linestyle='dashed',
linewidth=2,
label='mean'
)
plt.axvline(
x=processed_penguins_df.flipper_length_mm.median(),
color='blue',
linestyle='dashed',
linewidth=2,
label='median'
)
plt.axvline(
x=processed_penguins_df.flipper_length_mm.mode().values[0],
color='black',
linestyle='dashed',
linewidth=4,
label='mode'
)
plt.axvline(
x=processed_penguins_df.flipper_length_mm.quantile(0.25),
color='yellow',
linestyle='dashed',
linewidth=2,
label='Q1'
)
plt.axvline(
x=processed_penguins_df.flipper_length_mm.quantile(0.75),
color='green',
linestyle='dashed',
linewidth=2,
label='Q3'
)
plt.legend()
plt.show()
Distribuciones: PMFs, CDFs y PDFs
- Histograma.
- Función de probabilidad de masas (PMFs). Nos dice la probabilidad de que una variable aleatoria discreta tome un valor determinado.
- Función de distribución acumulada (CDFs). Devuelve la probabilidad de que una variable sea igual o menor que un valor determinado.
- Función de probabilidad de densidad (PDFs). Determina la probabilidad de que una variable continua tome un valor determinado.
Ley de los Grandes Números: La probabilidad experimental tiende a la probabilidad teórica a medida que aumenta el número de repeticiones del experimento.
Teorema del Límite Central: La media de las muestras tiende aproximadamente a una distribución normal. La suma de n variables aleatorias independientes con medias y varianzas finitas converge en distribución a una variable aleatoria con distribución normal.
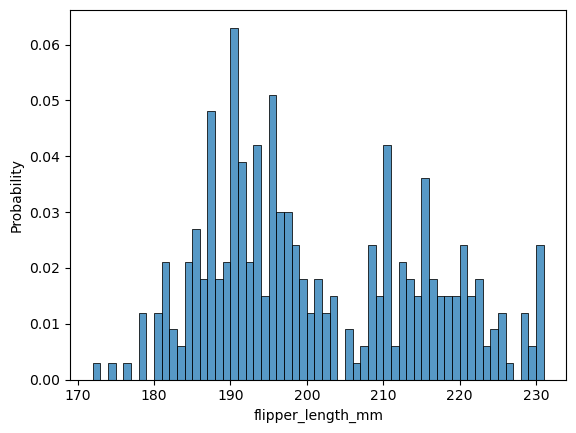
Funciones de probabilidad de masas (PMFs)
Utilizando seaborn
sns.histplot(
data=processed_penguins_df,
x='flipper_length_mm',
binwidth=1,
stat='probability' # Pasamos de freq a prob
)
plt.show()
Utilizando empiricaldist
pmf_flipper_length_mm = empiricaldist.Pmf.from_seq(
processed_penguins_df.flipper_length_mm,
normalize=True # Normalizamos la distribución para obtener probabilidades
)
pmf_flipper_length_mm.bar()
plt.show()
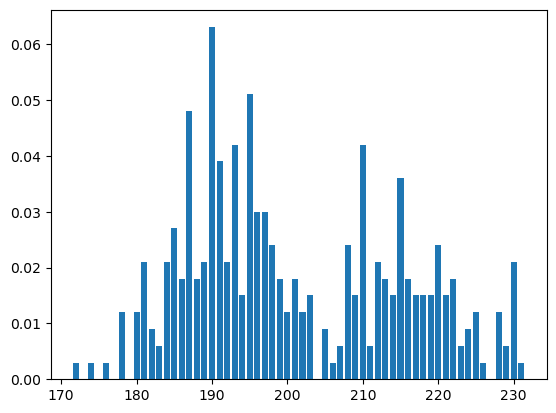
Tener mucho cuidado con Seaborn pues puede colapsar los valores extremos.
print(f"Probabilidad de longitud de ala -> 231: {pmf_flipper_length_mm(231)}")
Probabilidad de longitud de ala -> 231: 0.003003003003003003
processed_penguins_df.flipper_length_mm.max()
231.0
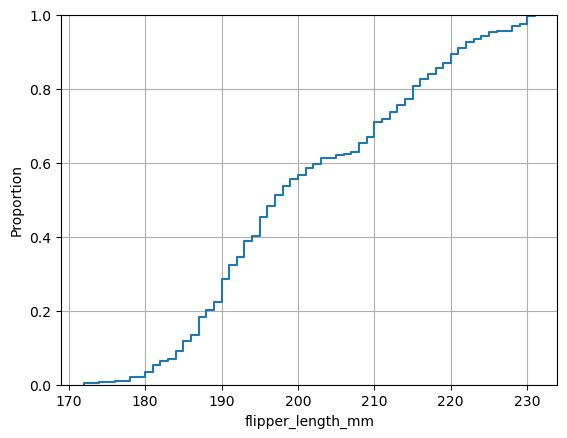
Funciones empirícas de probabilidad acumulada (ECDFs)
Empleando Seaborn
sns.ecdfplot(
data=processed_penguins_df,
x="flipper_length_mm"
)
plt.grid()
plt.show()
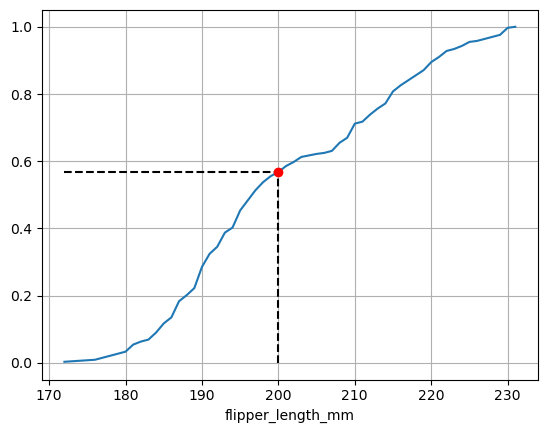
Utilizando empiricaldist
cdf_flipper_length_mm = empiricaldist.Cdf.from_seq(
processed_penguins_df.flipper_length_mm,
normalize=True
)
cdf_flipper_length_mm.plot()
q = 200 # Specify quantity
p = cdf_flipper_length_mm.forward(q)
plt.vlines(
x=q,
ymin=0,
ymax=p,
color = 'black',
linestyle='dashed'
)
plt.hlines(
y=p,
xmin=pmf_flipper_length_mm.qs[0],
xmax=q,
color='black',
linestyle='dashed'
)
plt.grid()
plt.plot(q, p, 'ro')
plt.show()
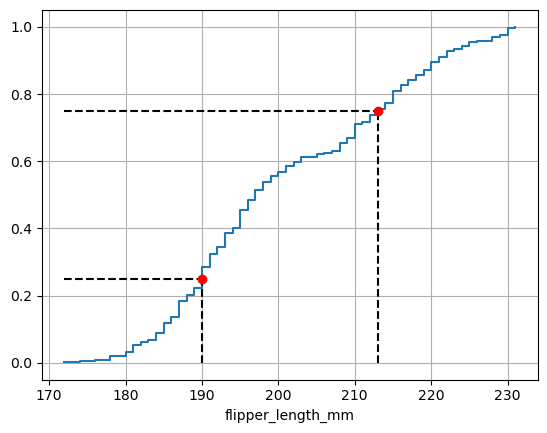
cdf_flipper_length_mm.step()
p_1 = 0.25 # Specify probability
p_2 = 0.75
ps = (0.25, 0.75) # IQR
qs = cdf_flipper_length_mm.inverse(ps)
plt.vlines(
x=qs,
ymin=0,
ymax=ps,
color = 'black',
linestyle='dashed'
)
plt.hlines(
y=ps,
xmin=pmf_flipper_length_mm.qs[0],
xmax=qs,
color='black',
linestyle='dashed'
)
plt.scatter(
x=qs,
y=ps,
color='red',
zorder=2
)
plt.grid()
plt.show()
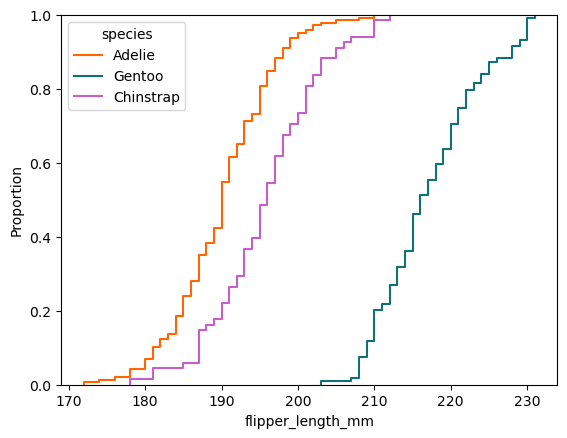
Comparando distribuciones
sns.ecdfplot(
data=processed_penguins_df,
x='flipper_length_mm',
hue='species',
palette=penguin_color
)
plt.show()
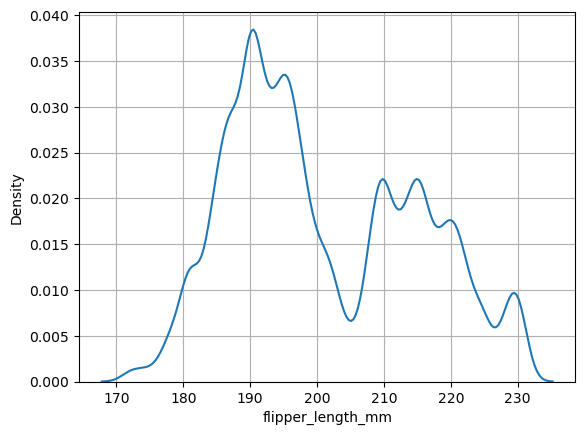
Funciones de densidad de probabilidad
sns.kdeplot(
data=processed_penguins_df,
x='flipper_length_mm',
bw_method=0.1
)
plt.grid()
plt.show()
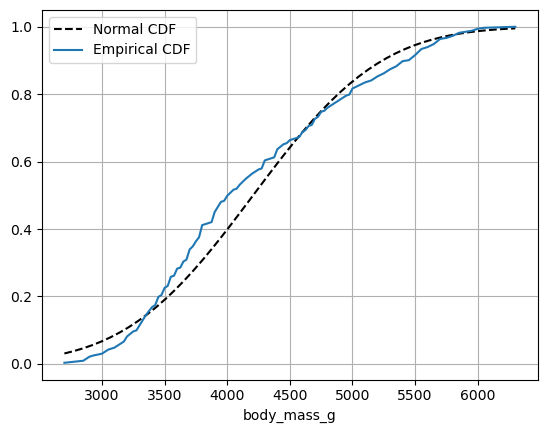
stats = processed_penguins_df.body_mass_g.describe()
stats
count 333.000000
mean 4207.057057
std 805.215802
min 2700.000000
25% 3550.000000
50% 4050.000000
75% 4775.000000
max 6300.000000
Name: body_mass_g, dtype: float64
import scipy
np.random.seed(42)
xs = np.linspace(stats['min'], stats['max'])
# CDF de la distribución normal
ys = scipy.stats.norm(stats['mean'], stats['std']).cdf(xs)
plt.plot(xs, ys, color='black', linestyle='dashed', label='Normal CDF')
empiricaldist.Cdf.from_seq(
processed_penguins_df.body_mass_g,
normalize=True
).plot(label='Empirical CDF')
plt.legend()
plt.grid()
plt.show()
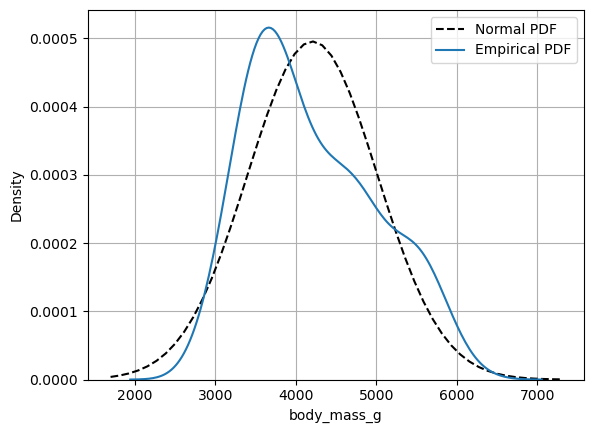
xs = np.linspace(stats['min']-1000, stats['max'] + 1000)
ys = scipy.stats.norm(stats['mean'], stats['std']).pdf(xs)
plt.plot(xs, ys, color='black', linestyle='dashed', label='Normal PDF')
sns.kdeplot(
data=processed_penguins_df,
x='body_mass_g',
label='Empirical PDF',
)
plt.legend()
plt.grid()
plt.show()
Teorema del límite central
processed_penguins_df.sex.value_counts(normalize=True)
sex
male 0.504505
female 0.495495
Name: proportion, dtype: float64
sex_numeric = processed_penguins_df.sex.replace({'male': 1, 'female': 0})
sex_numeric
0 1
1 0
2 0
4 0
5 1
..
339 1
340 0
341 1
342 1
343 0
Name: sex, Length: 333, dtype: int64
number_samples = 1000
sample_size=35
samples = []
np.random.seed(42)
for i in range(1, number_samples + 1):
sex_numeric_sample = sex_numeric.sample(sample_size, replace=True).to_numpy()
samples.append(pd.Series(sex_numeric_sample, name=f"sample_{i}"))
samples_df = pd.concat(samples, axis=1)
male_population_mean = samples_df.mean(numeric_only=True).mean()
print(f"Estimated percentage of male penguins in population is: {male_population_mean * 100:.4f}%")
Estimated percentage of male penguins in population is: 50.1829%
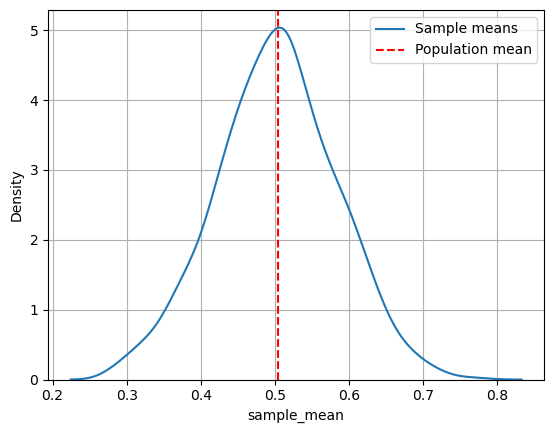
samples_df_numeric = samples_df.replace(['male', 'female'], [1, 0])
# Calculate the mean of each sample
sample_means_binomial = pd.DataFrame(samples_df_numeric.mean(),
columns=['sample_mean'])
# Plot the distribution of sample means
sns.kdeplot(data=sample_means_binomial, x='sample_mean', label='Sample means')
# Plot the population mean
plt.axvline(x=sex_numeric.replace(['male', 'female'], [1, 0]).mean(),
color='red', linestyle='dashed', label='Population mean')
plt.grid()
plt.legend()
plt.show()
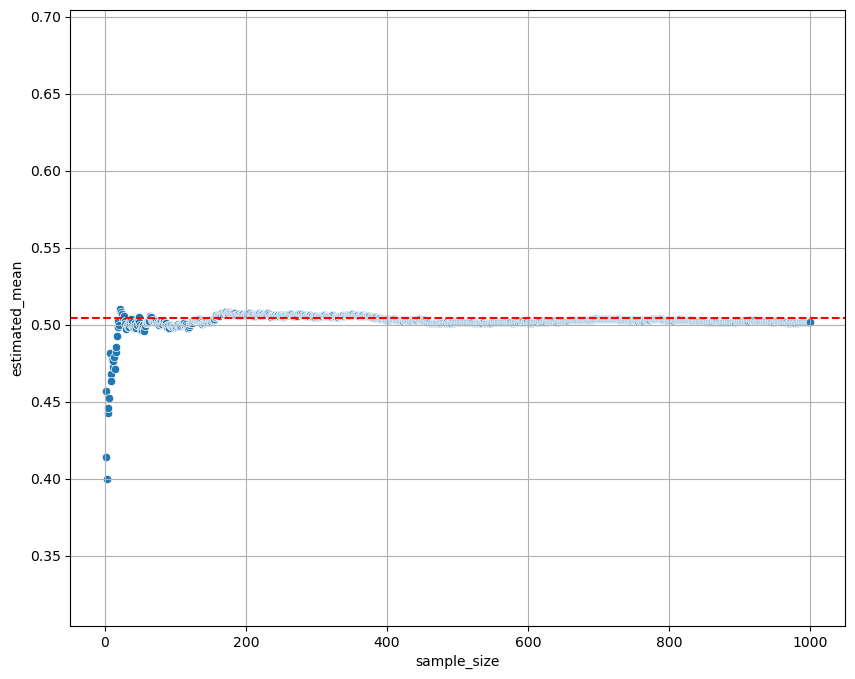
sample_size_experiment = pd.DataFrame(
[[i, samples_df.iloc[:, 0:i].mean().mean().mean()] for i in range(1, number_samples + 1)],
columns=['sample_size', 'estimated_mean']
)
plt.figure(figsize=(10, 8))
sns.scatterplot(
data=sample_size_experiment,
x='sample_size',
y='estimated_mean'
)
plt.axhline(
y=sex_numeric.mean(),
color='red',
linestyle='dashed'
)
plt.ylim([sex_numeric.mean() - 0.20, sex_numeric.mean() + 0.20])
plt.grid()
plt.show()
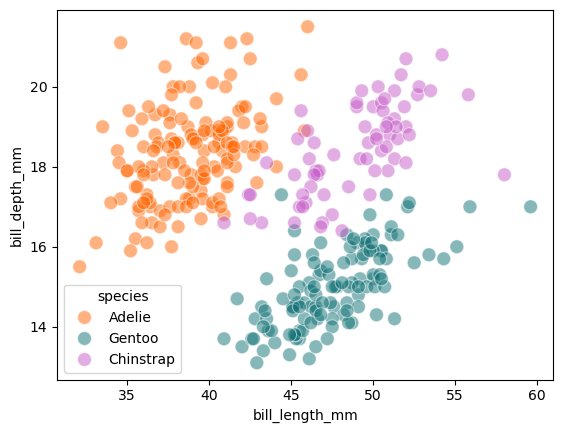
Análisis bivariado
Vemos la grafica de puntos, para entender las relaciones entre dos variables. Puede que obtengamos gráficos que no se ven bien. Es decir, muchos puntos convergen en una región evitando una buena visualización.
Una buena alternativa es variar la transparencia de los puntos (En Python alpha). Podemos emplear histogramas permitiendo una mejor visualización, además de jugar con paletas de colores.
Estableciendo relaciones: Gráfica de puntos
sns.scatterplot(
data=processed_penguins_df,
x='bill_length_mm',
y='bill_depth_mm',
hue='species',
palette=penguin_color,
alpha=0.5,
s=100
)
plt.show()
sns.displot(
data=processed_penguins_df,
x='bill_length_mm',
y='bill_depth_mm',
hue='species',
palette=penguin_color,
rug=True
)
plt.show()

En este gráfica observamos mejor donde se acumulan los datos.
sns.displot(
data=processed_penguins_df,
x='bill_length_mm',
y='bill_depth_mm',
hue='species',
palette=penguin_color,
kind='kde',
rug=True
)
plt.show()
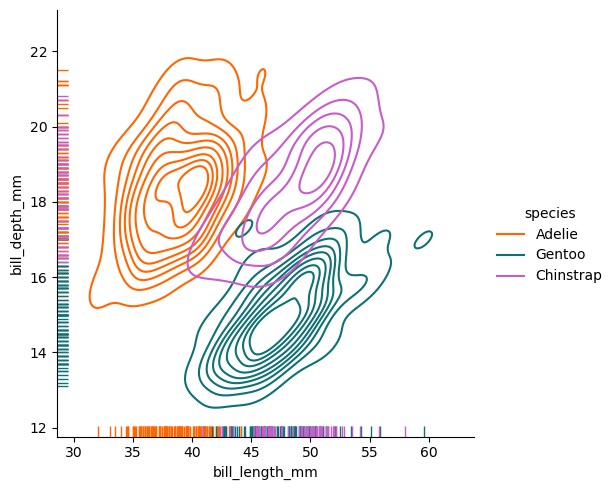
En este podemos observar las densidades de acumulación de la población de pinguinos.
sns.jointplot(
data=processed_penguins_df,
x='bill_length_mm',
y='bill_depth_mm',
)
plt.show()
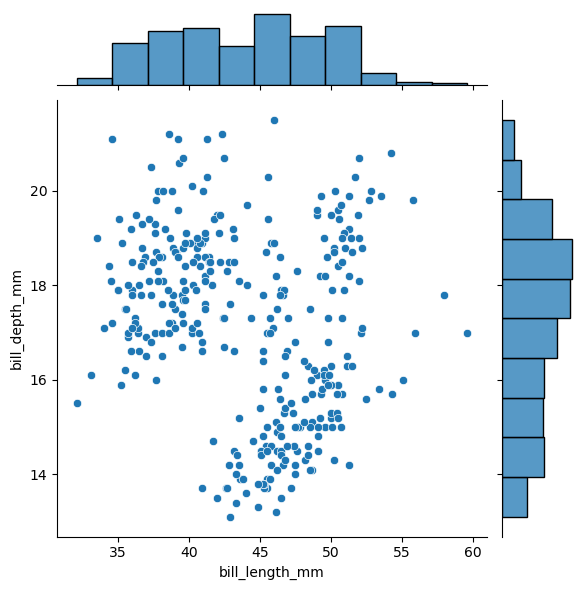
Mejorando la visualización
sns.jointplot(
data=processed_penguins_df,
x='bill_length_mm',
y='bill_depth_mm',
hue='species',
palette=penguin_color,
)
plt.show()
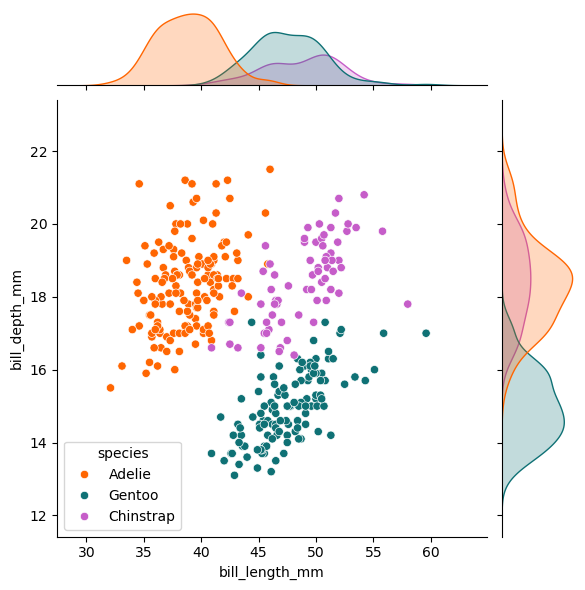
Estableciendo relaciones: gráficos de violín y boxplots
Un situación particular es cuando tenemos variables discretas, pues el scatter plot serán líneas. Podemos agregar un poco de ruido aleatorio con el objetivo de mejorar la visualización de los datos. Una buena forma de visualizar elegantemente son los boxplots y de violín.
sns.scatterplot(
data=processed_penguins_df,
x='species',
y='flipper_length_mm',
hue='species',
palette=penguin_color
)
plt.show()
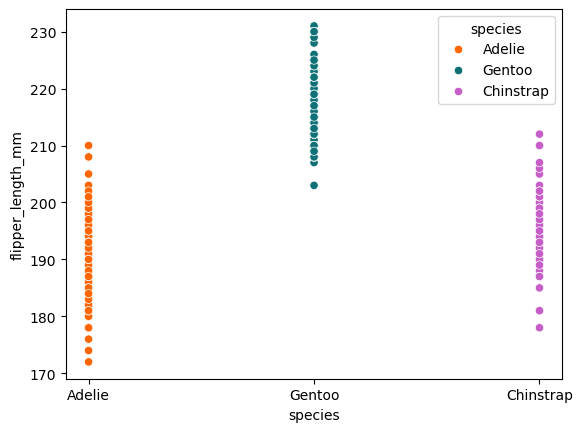
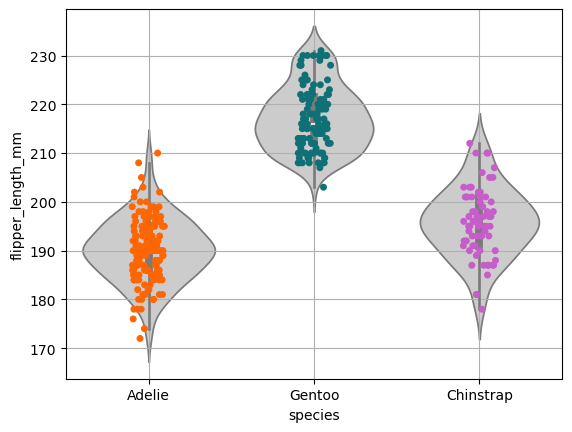
sns.stripplot(
data=processed_penguins_df,
x='species',
y='flipper_length_mm',
hue='species',
palette=penguin_color
)
plt.grid()
plt.show()
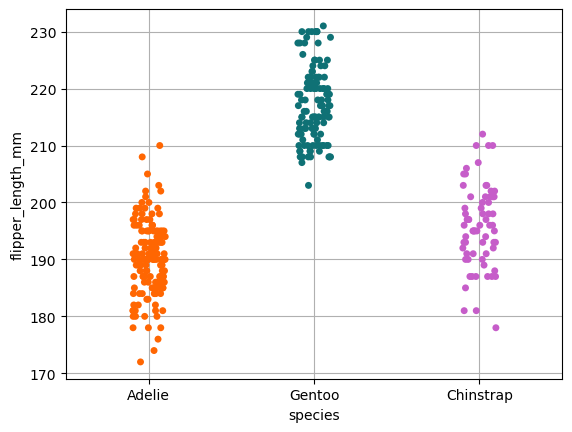
sns.boxplot(
data=processed_penguins_df,
x='flipper_length_mm',
y='species',
hue='species',
palette=penguin_color
)
plt.grid()
plt.show()
La idea es mejor esta visualización pues perdimos de vista la distribución de los datos.
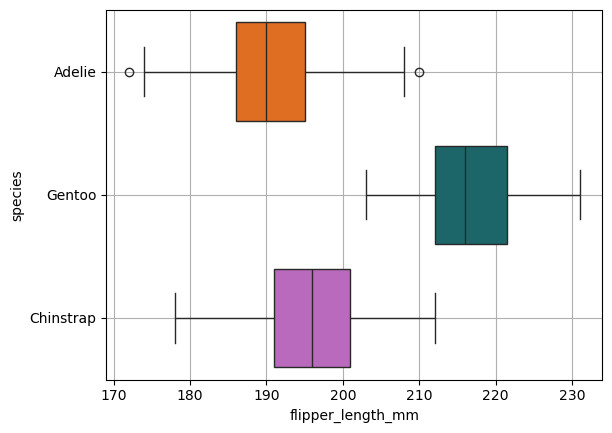
ax = sns.boxplot(
data=processed_penguins_df,
x='flipper_length_mm',
y='species',
hue='species',
palette=penguin_color
)
ax = sns.stripplot(
data=processed_penguins_df,
x='flipper_length_mm',
y='species',
color='.3'
)
plt.grid()
plt.show()
Obsersevamos mejor la distribución además de obtener otros estadístico como la media.
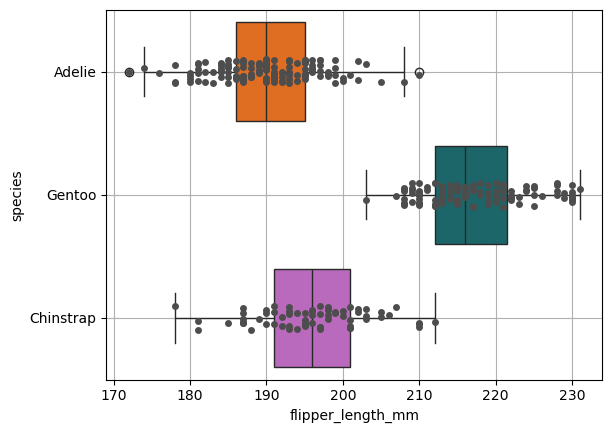
ax = sns.violinplot(
data=processed_penguins_df,
x='species',
y='flipper_length_mm',
color='.8'
)
ax = sns.stripplot(
data=processed_penguins_df,
x='species',
y='flipper_length_mm',
hue='species',
palette=penguin_color
)
plt.grid()
plt.show()
El siguiente gráfico apila los datos con igual valor apra observar mejor la distribución
sns.swarmplot(
data=processed_penguins_df,
x='species',
y='flipper_length_mm',
hue='species',
palette=penguin_color
)
plt.grid()
plt.show()
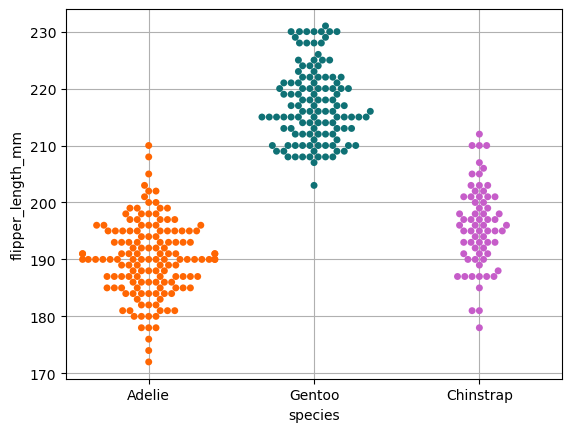
# Crear la rejilla para las facetas
g = sns.FacetGrid(data=processed_penguins_df,
col="island",
sharey=True,
sharex=True,
)
# Añadir el gráfico de violín a cada faceta
g.map_dataframe(
sns.violinplot,
x="species",
y="body_mass_g",
color=".8",
inner=None
)
# Añadir el gráfico de dispersión (stripplot) encima de los violines
g.map_dataframe(
sns.stripplot,
x="species",
y="body_mass_g",
hue="species",
palette=penguin_color,
)
# Ajustar leyendas y visualización
g.add_legend()
plt.show()
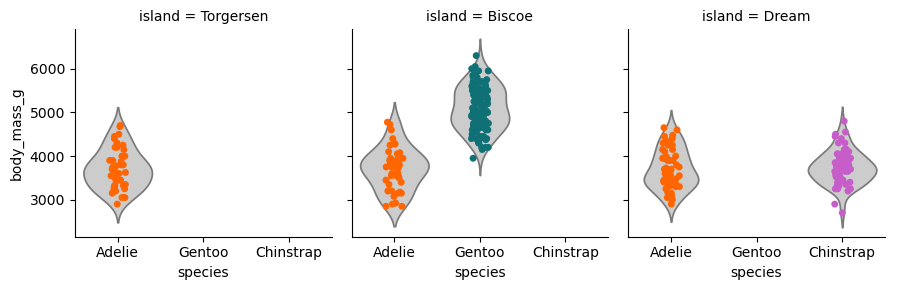
Estableciendo relaciones: matrices de correlación
Expresa hasta qué punto dos variables están relacionadas entre sí. Es decir, si cambian conjuntamente.
Coeficiente de correlación: cuantifica la intensidad de la relación lineal entre dos variables en un análisis decorrelación.
Importante: correlación no implica causalidad
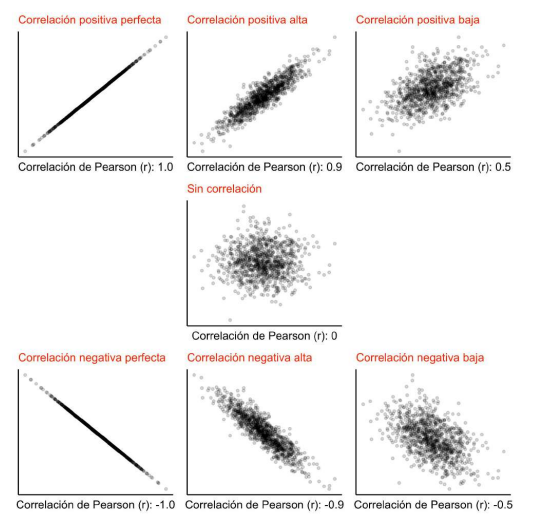
processed_penguins_df.corr(numeric_only=True)
| bill_length_mm | bill_depth_mm | flipper_length_mm | body_mass_g | year | |
|---|---|---|---|---|---|
| bill_length_mm | 1.000000 | -0.228626 | 0.653096 | 0.589451 | 0.032657 |
| bill_depth_mm | -0.228626 | 1.000000 | -0.577792 | -0.472016 | -0.048182 |
| flipper_length_mm | 0.653096 | -0.577792 | 1.000000 | 0.872979 | 0.151068 |
| body_mass_g | 0.589451 | -0.472016 | 0.872979 | 1.000000 | 0.021862 |
| year | 0.032657 | -0.048182 | 0.151068 | 0.021862 | 1.000000 |
sns.heatmap(
data=processed_penguins_df.corr(numeric_only=True),
cmap=sns.diverging_palette(20, 230, as_cmap=True),
center=0,
vmin=-1,
vmax=1,
linewidths=0.5,
cbar_kws={"shrink": 0.5},
annot=True
)
plt.show()
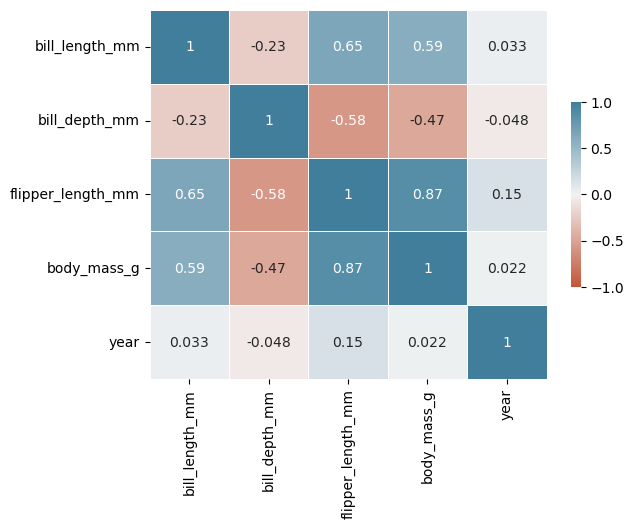
La línea cmap=sns.diverging_palette(20, 230, as_cmap=True) en el contexto de la función sns.heatmap() de Seaborn se utiliza para definir el mapa de colores (colormap) que se aplicará al gráfico de calor. Aquí te explico cada parte de esta línea:
- sns.diverging_palette(20, 230, as_cmap=True):
- sns.diverging_palette: Es una función de Seaborn que genera un paleta de colores divergente. Este tipo de paleta es útil cuando se quieren representar valores que se desvían de un punto central, como 0 en este caso.
- 20: Este es el valor del color en el ángulo de la rueda de colores para el primer color (en el espacio HSL). En este caso, corresponde a un tono de amarillo claro.
- 230: Este es el valor del color para el segundo color, que en este caso se corresponde con un tono azul claro.
- as_cmap=True: Esto indica que se debe devolver la paleta como un objeto de colormap que Seaborn y Matplotlib pueden utilizar directamente para el gráfico.
- Uso en sns.heatmap:
- La paleta divergente creada se usará para mapear los valores de la matriz de correlación
data=processed_penguins_df.corr(numeric_only=True). - Los colores irán desde el color definido por el primer valor (20, amarillo) hasta el definido por el segundo valor (230, azul), pasando por un tono neutro en el centro (0). Esto permite visualizar fácilmente las correlaciones positivas y negativas.
- La paleta divergente creada se usará para mapear los valores de la matriz de correlación
sns.clustermap(
data=processed_penguins_df.corr(numeric_only=True),
cmap=sns.diverging_palette(20, 230, as_cmap=True),
center=0,
vmin=-1,
vmax=1,
linewidths=0.5,
cbar_kws={"shrink": 0.5},
annot=True
)
plt.show()
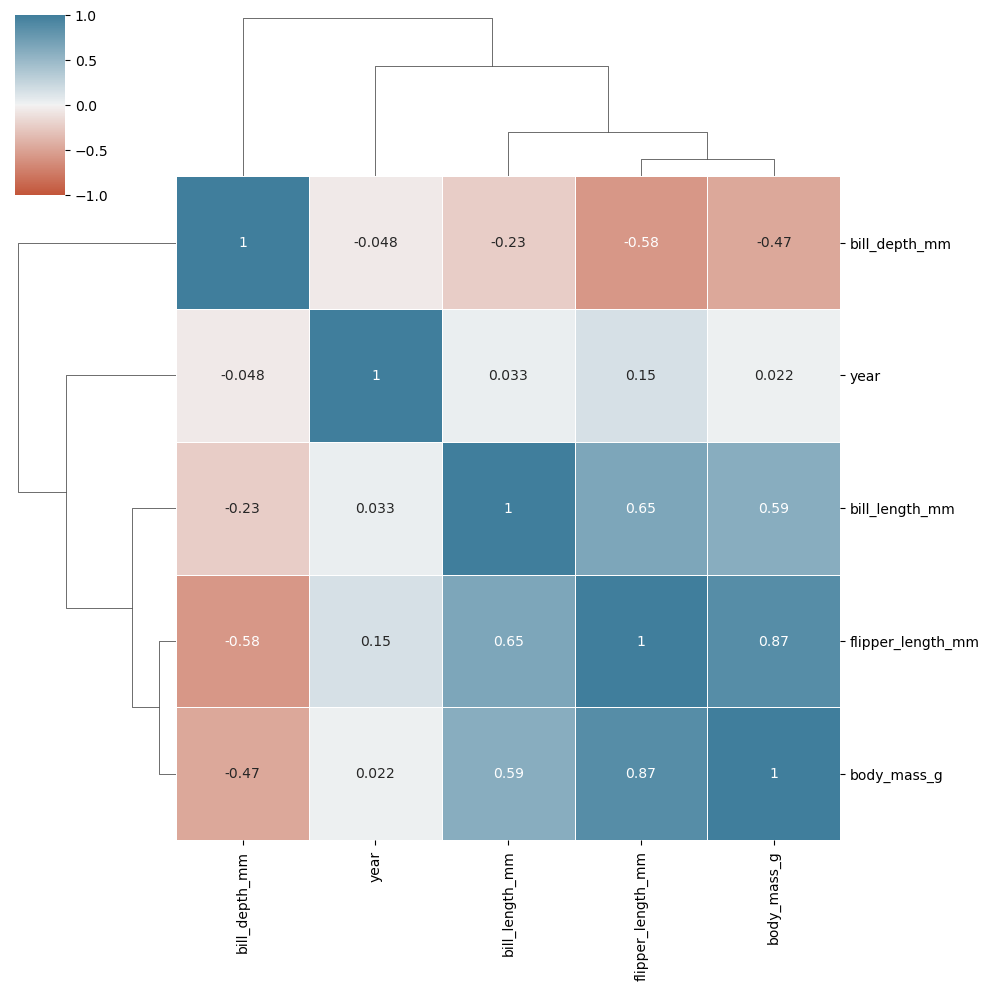
La diferencia entre heatmap y clustermap en Seaborn se centra en la forma en que se presentan los datos y en la adición de información sobre las relaciones entre las variables.
Heatmap
Definición: Un
heatmapes una representación gráfica de datos en forma de matriz, donde los valores se representan mediante colores. Es útil para visualizar la intensidad de los valores en una matriz.Uso: Se utiliza principalmente para mostrar la correlación entre variables, frecuencias o cualquier otro tipo de datos tabulares.
Estructura: No incluye agrupamiento; simplemente representa los datos tal como están. Esto significa que no se reorganizan las filas o columnas en función de similitudes.
Ejemplo de uso: Visualizar una matriz de correlación entre variables de un conjunto de datos.
Clustermap
Definición: Un
clustermapes similar a unheatmap, pero incluye un análisis de agrupamiento jerárquico. Esto significa que las filas y/o columnas se reorganizan en función de sus similitudes.Uso: Se utiliza para identificar patrones y agrupaciones en los datos, permitiendo que se visualicen relaciones que no son evidentes en un simple
heatmap.Estructura: Las filas y/o columnas se agrupan usando algoritmos de clustering (como el método de enlace completo o enlace sencillo), lo que puede ayudar a identificar grupos de datos similares.
Ejemplo de uso: Identificar grupos de especies en un conjunto de datos biológicos según sus características medibles, mostrando tanto la intensidad de las medidas como las relaciones entre las diferentes especies.
¿Cómo podría representar una variable categórica como numérica discreta?
processed_penguins_df = (
processed_penguins_df
.assign(
numeric_sex=lambda df: df.sex.map({'male': 1, 'female': 0})
)
)
Mejor usar map que replace nos evita un warning.
sns.clustermap(
data=processed_penguins_df.corr(numeric_only=True),
cmap= sns.diverging_palette(20, 230, as_cmap=True), # 'BrBG'
center=0,
vmin=-1,
vmax=1,
linewidths=0.5,
cbar_kws={"shrink": 0.5},
annot=True
)
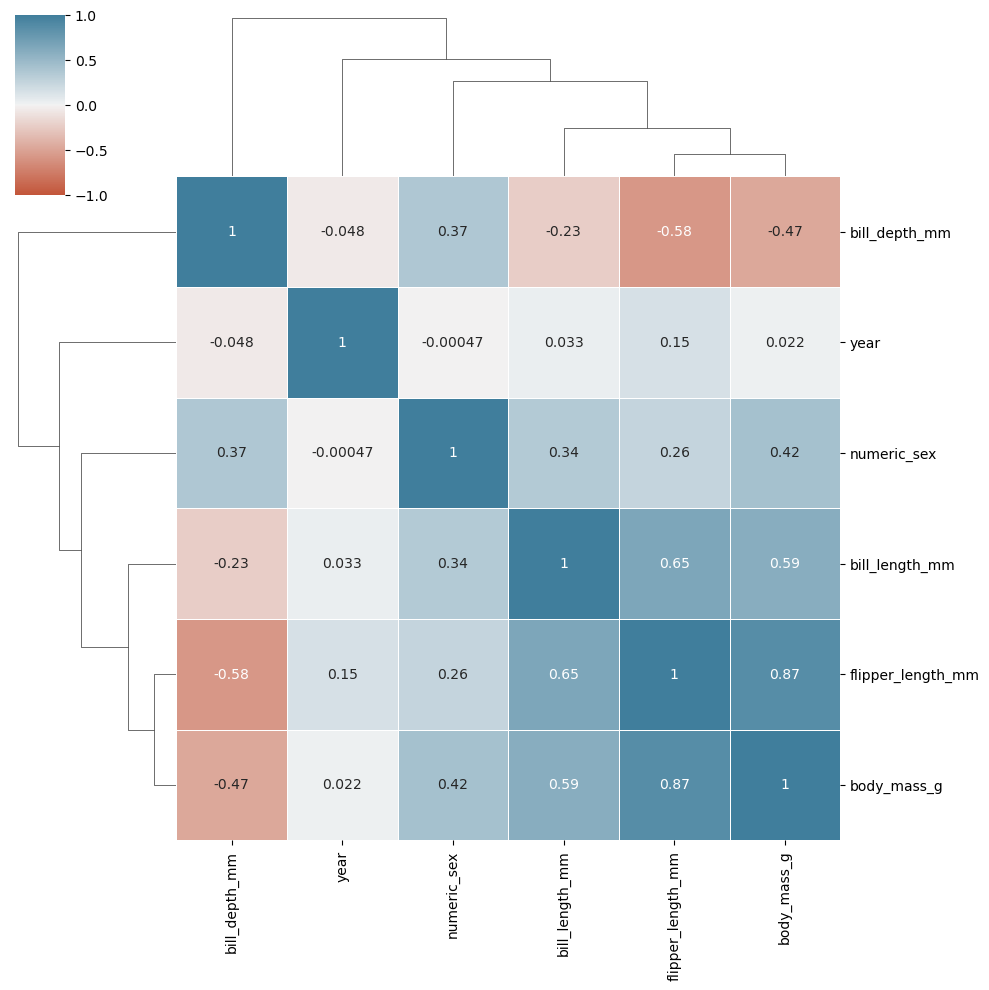
Limitantes de los coeficientes de correlación lineal
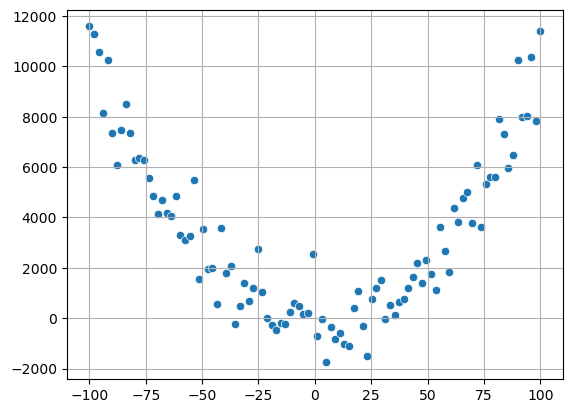
El coeficiente de correlación lineal nos ayuda a determinar la posible existencia de una correlación lineal, sin embargo, su ausencia no significa que no exista otro tipo de correlación.
x = np.linspace(-100, 100, 100)
y = x ** 2
y += np.random.normal(0, 1000, x.size)
sns.scatterplot(x=x, y=y)
print(f"Coef corr: \n{np.corrcoef(x, y)}")
plt.grid()
plt.show()
Coef corr:
[[ 1. -0.07336699]
[-0.07336699 1. ]]
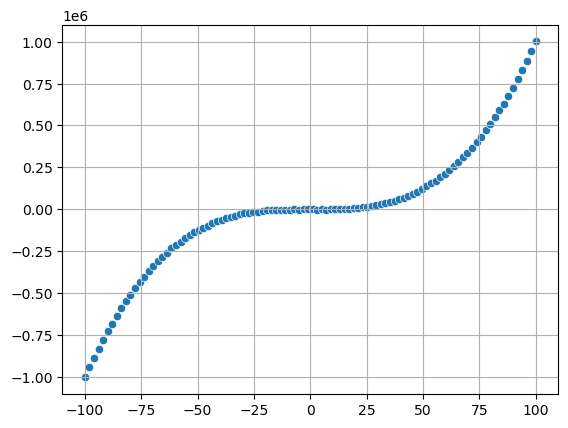
x = np.linspace(-100, 100, 100)
y = x ** 3
y += np.random.normal(0, 1000, x.size)
sns.scatterplot(x=x, y=y)
print(f"Coef corr: \n{np.corrcoef(x, y)}")
plt.grid()
plt.show()
Coef corr:
[[1. 0.9165443]
[0.9165443 1. ]]
sns.scatterplot(
data=processed_penguins_df,
x='bill_length_mm',
y='bill_depth_mm'
)
plt.show()
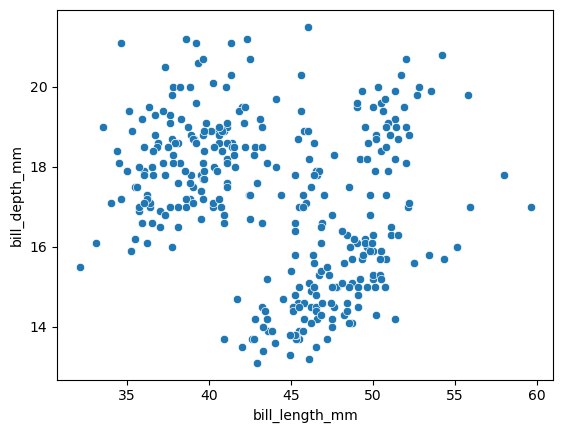
El coeficiente de correlación no nos habla del impacto de la relación
El coeficiente de correlación es una medida estadística que indica la fuerza y la dirección de una relación lineal entre dos variables. Sin embargo, hay algunos aspectos importantes que hay que considerar sobre lo que este coeficiente realmente representa:
Relación vs. Causalidad: Un coeficiente de correlación alto no implica que una variable cause cambios en la otra. Puede haber factores ocultos o variables de confusión que afectan ambas. Por ejemplo, una alta correlación entre el consumo de helados y las tasas de ahogamiento no significa que uno cause el otro; ambos pueden estar relacionados con el clima cálido.
No Captura el Impacto: Aunque el coeficiente puede mostrar que dos variables están relacionadas, no indica la magnitud del efecto que tiene una variable sobre la otra. Por ejemplo, una correlación de 0.8 entre horas de estudio y calificaciones puede sugerir una fuerte relación, pero no nos dice cuánto mejorará la calificación si se incrementan las horas de estudio.
Sensibilidad a Valores Atípicos: La correlación puede ser influenciada por valores atípicos, que pueden distorsionar la percepción de la relación entre las variables. Un único valor extremo puede hacer que la correlación se vea mucho más fuerte o más débil de lo que realmente es.
Limitaciones en la Interpretación: El coeficiente de correlación se limita a relaciones lineales. Si la relación es no lineal, el coeficiente podría ser bajo a pesar de que exista una relación significativa entre las variables.
np.random.seed(42)
x_1 = np.linspace(0, 100, 100)
y_1 = 0.1 * x_1 + 3 + np.random.uniform(-2, 2, size=x_1.size)
sns.scatterplot(
x=x_1,
y=y_1
)
x_2 = np.linspace(0, 100, 100)
y_2 = 0.5 * x_2 + 1 + np.random.uniform(0, 60, size=x_2.size)
sns.scatterplot(
x=x_2,
y=y_2
)
plt.legend(labels=['1', '2'])
print(np.corrcoef(x_1, y_1))
print(np.corrcoef(x_2, y_2))
plt.show()
[[1. 0.92761617]
[0.92761617 1. ]]
[[1. 0.67476343]
[0.67476343 1. ]]
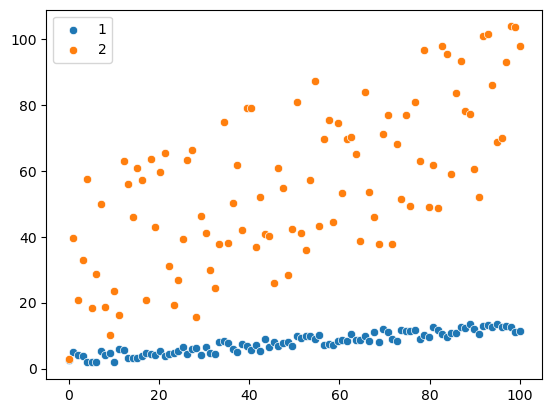
Observamos en esta gráfica, que los datos azules representan una mayor correlación, pero en cuanto impacto es menor que los datos naranjas. Por tanto, siempre debemos revisar el impacto de las variables correlacionadas, pues el coeficiente de correlación no lo refleja.
Estableciendo relaciones: análisis de regresión simple
Nota para leer: ¿Cuál es la matemática detrás de la regresión lineal?
En el ejemplo x_1, y_1, x_2, y_2 generados con anterioridad para el ejemplo anterior.
res_1 = scipy.stats.linregress(x=x_1, y=y_1)
res_2 = scipy.stats.linregress(x=x_2, y=y_2)
print(res_1, res_2, sep="\n")
LinregressResult(slope=0.1008196928097962, intercept=2.8397383330230257, rvalue=0.9276161661149585, pvalue=1.0607043467839354e-43, stderr=0.004101050284084737, intercept_stderr=0.23737141027424583)
LinregressResult(slope=0.5470008424819229, intercept=28.51986126520522, rvalue=0.6747634267657531, pvalue=1.3883699878991933e-14, stderr=0.060436575031364535, intercept_stderr=3.4981075708858227)
Podemos observar que el slope del segundo conjunto de datos, color naranja, es mayor que el slope del conjunto de datos de color azul. Por tanto crece más, por tanto existe una mejor relación entre esas variables.
sns.scatterplot(
x=x_1,
y=y_1
)
fx_1 = np.array([x_1.min(), x_1.max()])
fy_1 = res_1.intercept + res_1.slope * fx_1
plt.plot(fx_1, fy_1)
sns.scatterplot(
x=x_2,
y=y_2
)
fx_2 = np.array([x_2.min(), x_2.max()])
fy_2 = res_2.intercept + res_2.slope * fx_2
plt.plot(fx_2, fy_2)
plt.legend(labels=['1', '1', '2', '2'])
plt.show()
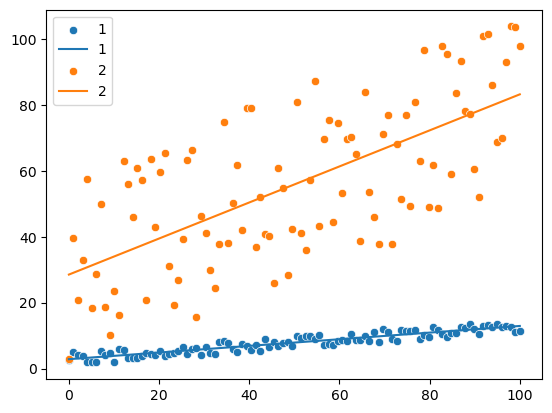
sns.scatterplot(
data=processed_penguins_df,
x='bill_length_mm',
y='bill_depth_mm'
)
res_penguins = scipy.stats.linregress(x=processed_penguins_df.bill_length_mm,
y=processed_penguins_df.bill_depth_mm)
print(res_penguins)
fx_1 = np.array([processed_penguins_df.bill_length_mm.min(),
processed_penguins_df.bill_length_mm.max()])
fy_1 = res_penguins.intercept + res_penguins.slope * fx_1
plt.plot(fx_1, fy_1)
plt.grid()
plt.show()
LinregressResult(slope=-0.08232675339862278, intercept=20.78664866843383, rvalue=-0.22862563591302912, pvalue=2.528289720944301e-05, stderr=0.01926834673577886, intercept_stderr=0.8541730787409803)
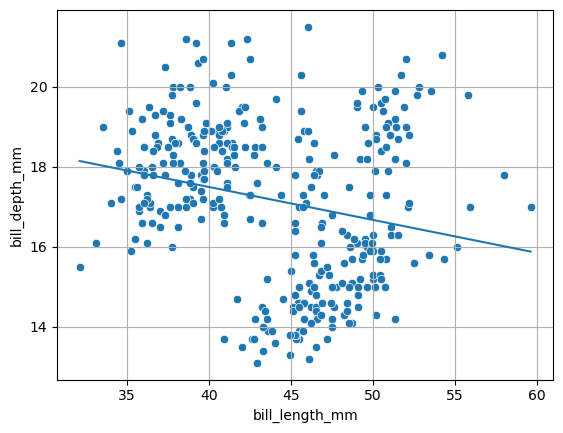
sns.lmplot(
data=processed_penguins_df,
x='bill_length_mm',
y='bill_depth_mm',
height=6
)
plt.show()
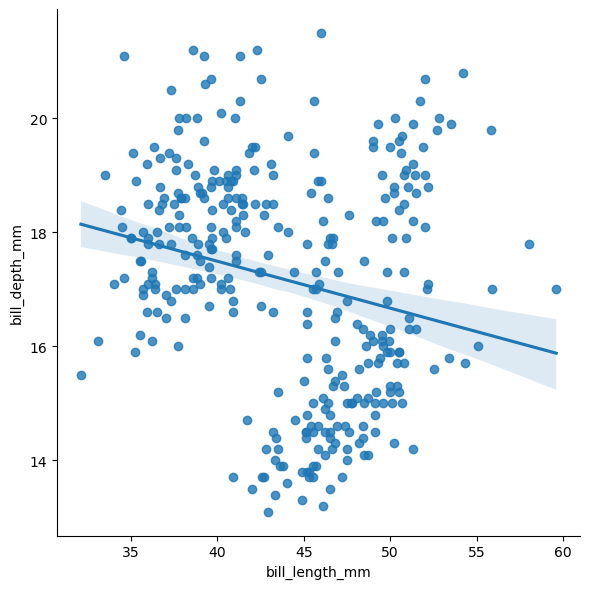
Limitaciones del análisis de regresión simple
La regresión lineal simple de A con B no es lo mismo que la de B con A. Si dos variables crecen o decrecen siguiendo las mismas pautas, no implica necesariamente que una cause la otra.
x = processed_penguins_df.bill_length_mm
y = processed_penguins_df.bill_depth_mm
res_x_y = scipy.stats.linregress(x=x, y=y)
res_y_x = scipy.stats.linregress(x=y, y=x)
print(res_x_y, res_y_x, sep="\n")
LinregressResult(slope=-0.08232675339862278, intercept=20.78664866843383, rvalue=-0.22862563591302912, pvalue=2.528289720944301e-05, stderr=0.01926834673577886, intercept_stderr=0.8541730787409803)
LinregressResult(slope=-0.6349051704195025, intercept=54.89085424504756, rvalue=-0.22862563591302912, pvalue=2.528289720944301e-05, stderr=0.14859778216623315, intercept_stderr=2.5673415135382562)
Observamos que no devuelve el mismo resultado, verificando que no es igual calcular estas correaciones.
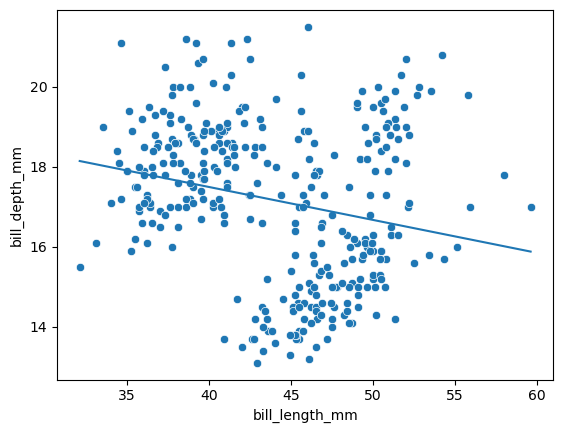
sns.scatterplot(
x=x,
y=y
)
fx_1 = np.array([x.min(), x.max()])
fy_1 = res_x_y.intercept + res_x_y.slope * fx_1
plt.plot(fx_1, fy_1)
plt.show()
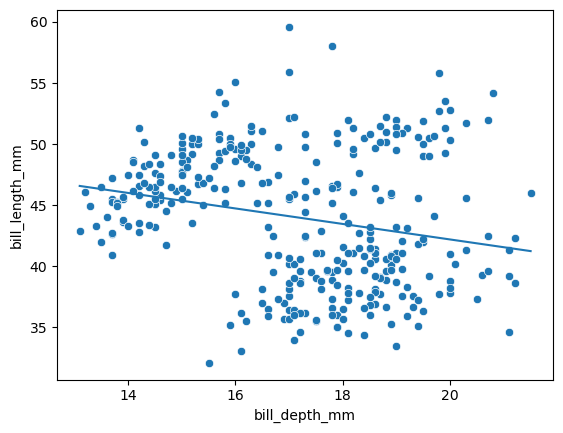
sns.scatterplot(
x=y,
y=x
)
fx_2 = np.array([y.min(), y.max()])
fy_2 = res_y_x.intercept + res_y_x.slope * fx_2
plt.plot(fx_2, fy_2)
[<matplotlib.lines.Line2D at 0x1d4ea09f450>]
sns.scatterplot(
x=x,
y=y
)
plt.plot(fx_1, fy_1)
plt.plot(fy_2, fx_2)
plt.show()
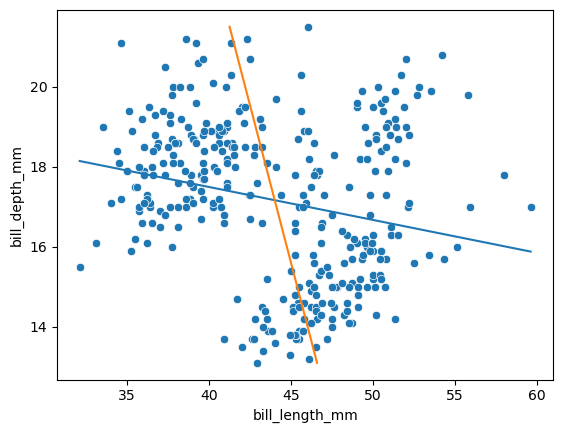
La regresión no nos dice nada sobre la causalidad, pero existen herramientas para separar las relaciones entre varias variables.
La pendiente es -0.634905, lo que significa que cada milímetro adicional de profundidad del pico es asociado a un decremento de -0.634905 milímetros de la longitud del pico de un pingüino.
(
smf.ols(
formula="bill_length_mm ~ bill_depth_mm",
data=processed_penguins_df
)
.fit()
.params
)
Intercept 54.890854
bill_depth_mm -0.634905
dtype: float64
formula="bill_length_mm ~ bill_depth_mm": Laformulaespecifica el modelo de regresión. En este caso,bill_length_mmes la variable dependiente (o respuesta) que queremos predecir, ybill_depth_mmes la variable independiente (o explicativa) que se utiliza para hacer la predicción. El símbolo~se utiliza para separar la variable dependiente de la independiente.
(
smf.ols(
formula="bill_depth_mm ~ bill_length_mm",
data=processed_penguins_df
)
.fit()
.summary()
)
| Dep. Variable: | bill_depth_mm | R-squared: | 0.052 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.049 |
| Method: | Least Squares | F-statistic: | 18.26 |
| Date: | Thu, 19 Dec 2024 | Prob (F-statistic): | 2.53e-05 |
| Time: | 17:38:41 | Log-Likelihood: | -688.72 |
| No. Observations: | 333 | AIC: | 1381. |
| Df Residuals: | 331 | BIC: | 1389. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 20.7866 | 0.854 | 24.335 | 0.000 | 19.106 | 22.467 |
| bill_length_mm | -0.0823 | 0.019 | -4.273 | 0.000 | -0.120 | -0.044 |
| Omnibus: | 15.442 | Durbin-Watson: | 1.197 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 6.783 |
| Skew: | -0.014 | Prob(JB): | 0.0337 |
| Kurtosis: | 2.301 | Cond. No. | 360. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Análisis multivariado
Análisis de regresión múltiple
La regresión lineal y la regresión múltiple son técnicas estadísticas utilizadas para modelar la relación entre variables, pero tienen diferencias clave:
Regresión Lineal
- Descripción: Se utiliza para predecir el valor de una variable dependiente a partir de una sola variable independiente.
- Modelo: La relación se representa con una línea recta, siguiendo la fórmula ( Y = a + bX ), donde:
- ( Y ) es la variable dependiente.
- ( X ) es la variable independiente.
- ( a ) es la intersección (constante).
- ( b ) es la pendiente (coeficiente).
Regresión Múltiple
- Descripción: Se utiliza para predecir el valor de una variable dependiente a partir de múltiples variables independientes.
- Modelo: La relación se representa con una ecuación lineal múltiple, siguiendo la fórmula ( Y = a + b_1X_1 + b_2X_2 + … + b_nX_n ), donde:
- ( Y ) es la variable dependiente.
- ( X_1, X_2, …, X_n ) son las variables independientes.
- ( a ) es la intersección.
- ( b_1, b_2, …, b_n ) son los coeficientes asociados a cada variable.
Resumen
- Número de variables: La regresión lineal tiene una sola variable independiente, mientras que la regresión múltiple utiliza varias.
- Complejidad: La regresión múltiple puede capturar relaciones más complejas entre las variables, mientras que la regresión lineal es más simple y directa.
Olvidé mi báscula para pesar a los pingüinos, ¿Cuál sería la mejor forma de capturar ese dato?
Emplearemos varios modelos
model_1 = (
smf.ols(
formula="body_mass_g ~ bill_length_mm",
data=processed_penguins_df
)
.fit()
)
model_1.summary()
| Dep. Variable: | body_mass_g | R-squared: | 0.347 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.345 |
| Method: | Least Squares | F-statistic: | 176.2 |
| Date: | Thu, 19 Dec 2024 | Prob (F-statistic): | 1.54e-32 |
| Time: | 18:41:33 | Log-Likelihood: | -2629.1 |
| No. Observations: | 333 | AIC: | 5262. |
| Df Residuals: | 331 | BIC: | 5270. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 388.8452 | 289.817 | 1.342 | 0.181 | -181.271 | 958.961 |
| bill_length_mm | 86.7918 | 6.538 | 13.276 | 0.000 | 73.931 | 99.652 |
| Omnibus: | 6.141 | Durbin-Watson: | 0.849 |
|---|---|---|---|
| Prob(Omnibus): | 0.046 | Jarque-Bera (JB): | 4.899 |
| Skew: | -0.197 | Prob(JB): | 0.0864 |
| Kurtosis: | 2.555 | Cond. No. | 360. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Relacion de body_mass_g con bill_length_mm + bill_depth_mm
model_2 = (
smf.ols(
formula="body_mass_g ~ bill_length_mm + bill_depth_mm ",
data=processed_penguins_df
)
.fit()
)
model_2.summary()
| Dep. Variable: | body_mass_g | R-squared: | 0.467 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.464 |
| Method: | Least Squares | F-statistic: | 144.8 |
| Date: | Thu, 19 Dec 2024 | Prob (F-statistic): | 7.04e-46 |
| Time: | 18:41:45 | Log-Likelihood: | -2595.2 |
| No. Observations: | 333 | AIC: | 5196. |
| Df Residuals: | 330 | BIC: | 5208. |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 3413.4519 | 437.911 | 7.795 | 0.000 | 2552.002 | 4274.902 |
| bill_length_mm | 74.8126 | 6.076 | 12.313 | 0.000 | 62.860 | 86.765 |
| bill_depth_mm | -145.5072 | 16.873 | -8.624 | 0.000 | -178.699 | -112.315 |
| Omnibus: | 2.839 | Durbin-Watson: | 1.798 |
|---|---|---|---|
| Prob(Omnibus): | 0.242 | Jarque-Bera (JB): | 2.175 |
| Skew: | -0.000 | Prob(JB): | 0.337 |
| Kurtosis: | 2.604 | Cond. No. | 644. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
model_3 = (
smf.ols(
formula="body_mass_g ~ bill_length_mm + bill_depth_mm + flipper_length_mm",
data=processed_penguins_df
)
.fit()
)
model_3.summary()
| Dep. Variable: | body_mass_g | R-squared: | 0.764 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.762 |
| Method: | Least Squares | F-statistic: | 354.9 |
| Date: | Thu, 19 Dec 2024 | Prob (F-statistic): | 9.26e-103 |
| Time: | 18:42:27 | Log-Likelihood: | -2459.8 |
| No. Observations: | 333 | AIC: | 4928. |
| Df Residuals: | 329 | BIC: | 4943. |
| Df Model: | 3 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -6445.4760 | 566.130 | -11.385 | 0.000 | -7559.167 | -5331.785 |
| bill_length_mm | 3.2929 | 5.366 | 0.614 | 0.540 | -7.263 | 13.849 |
| bill_depth_mm | 17.8364 | 13.826 | 1.290 | 0.198 | -9.362 | 45.035 |
| flipper_length_mm | 50.7621 | 2.497 | 20.327 | 0.000 | 45.850 | 55.675 |
| Omnibus: | 5.596 | Durbin-Watson: | 1.982 |
|---|---|---|---|
| Prob(Omnibus): | 0.061 | Jarque-Bera (JB): | 5.469 |
| Skew: | 0.312 | Prob(JB): | 0.0649 |
| Kurtosis: | 3.068 | Cond. No. | 5.44e+03 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 5.44e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Hasta acá observamos como la unión de varias variables hace que la realación cambie, por ejemplo el tamaño del pico en relación del peso daba una alta relación, pero al incluir otras variables ahora explica menos el peso del pinguino.
Es importante tener en cuenta el parámetro R-squared que nos dice cuanta variabilidad de los datos se estan ajustando. A mayor valor, nos indica cuan preciso es nuestro modelo.
model_4 = (
smf.ols(
formula="body_mass_g ~ bill_length_mm + bill_depth_mm + flipper_length_mm + C(sex)",
data=processed_penguins_df
)
.fit()
)
model_4.summary()
| Dep. Variable: | body_mass_g | R-squared: | 0.823 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.821 |
| Method: | Least Squares | F-statistic: | 381.3 |
| Date: | Thu, 19 Dec 2024 | Prob (F-statistic): | 6.28e-122 |
| Time: | 18:42:41 | Log-Likelihood: | -2411.8 |
| No. Observations: | 333 | AIC: | 4834. |
| Df Residuals: | 328 | BIC: | 4853. |
| Df Model: | 4 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -2288.4650 | 631.580 | -3.623 | 0.000 | -3530.924 | -1046.006 |
| C(sex)[T.male] | 541.0285 | 51.710 | 10.463 | 0.000 | 439.304 | 642.753 |
| bill_length_mm | -2.3287 | 4.684 | -0.497 | 0.619 | -11.544 | 6.886 |
| bill_depth_mm | -86.0882 | 15.570 | -5.529 | 0.000 | -116.718 | -55.459 |
| flipper_length_mm | 38.8258 | 2.448 | 15.862 | 0.000 | 34.011 | 43.641 |
| Omnibus: | 2.598 | Durbin-Watson: | 1.843 |
|---|---|---|---|
| Prob(Omnibus): | 0.273 | Jarque-Bera (JB): | 2.125 |
| Skew: | 0.062 | Prob(JB): | 0.346 |
| Kurtosis: | 2.629 | Cond. No. | 7.01e+03 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 7.01e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Es importante destacar que el parámetro C(sex)[T.male] 541.0285 nos dice la relación de los machos con las hembras, donde los machos en promedio pesan 541 gramos más que las hembras.
model_5 = (
smf.ols(
formula="body_mass_g ~ flipper_length_mm + C(sex)",
data=processed_penguins_df
)
.fit()
)
model_5.summary()
| Dep. Variable: | body_mass_g | R-squared: | 0.806 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.805 |
| Method: | Least Squares | F-statistic: | 684.8 |
| Date: | Thu, 19 Dec 2024 | Prob (F-statistic): | 3.53e-118 |
| Time: | 18:48:20 | Log-Likelihood: | -2427.2 |
| No. Observations: | 333 | AIC: | 4860. |
| Df Residuals: | 330 | BIC: | 4872. |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -5410.3002 | 285.798 | -18.931 | 0.000 | -5972.515 | -4848.085 |
| C(sex)[T.male] | 347.8503 | 40.342 | 8.623 | 0.000 | 268.491 | 427.209 |
| flipper_length_mm | 46.9822 | 1.441 | 32.598 | 0.000 | 44.147 | 49.817 |
| Omnibus: | 0.262 | Durbin-Watson: | 1.710 |
|---|---|---|---|
| Prob(Omnibus): | 0.877 | Jarque-Bera (JB): | 0.376 |
| Skew: | 0.051 | Prob(JB): | 0.829 |
| Kurtosis: | 2.870 | Cond. No. | 2.95e+03 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.95e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
Visualización del análisis de regresión múltiple
Tabla de resultados
models_results = pd.DataFrame(
dict(
actual_value=processed_penguins_df.body_mass_g,
prediction_model_1 = model_1.predict(),
prediction_model_2 = model_2.predict(),
prediction_model_3 = model_3.predict(),
prediction_model_4 = model_4.predict(),
prediction_model_5 = model_5.predict(),
species=processed_penguins_df.species,
sex=processed_penguins_df.sex
)
)
models_results
| actual_value | prediction_model_1 | prediction_model_2 | prediction_model_3 | prediction_model_4 | prediction_model_5 | species | sex | |
|---|---|---|---|---|---|---|---|---|
| 0 | 3750.0 | 3782.402961 | 3617.641192 | 3204.761227 | 3579.136946 | 3441.323750 | Adelie | male |
| 1 | 3800.0 | 3817.119665 | 3836.725580 | 3436.701722 | 3343.220772 | 3328.384372 | Adelie | female |
| 2 | 3250.0 | 3886.553073 | 3809.271371 | 3906.897032 | 3639.137335 | 3751.223949 | Adelie | female |
| 4 | 3450.0 | 3574.102738 | 3350.786581 | 3816.705772 | 3457.954243 | 3657.259599 | Adelie | female |
| 5 | 3650.0 | 3799.761313 | 3356.140070 | 3696.168128 | 3764.536023 | 3864.163327 | Adelie | male |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 339 | 4000.0 | 5231.825347 | 4706.954140 | 4599.187485 | 4455.022405 | 4662.860306 | Chinstrap | male |
| 340 | 3400.0 | 4164.286703 | 4034.121055 | 4274.552753 | 3894.857519 | 4080.099176 | Chinstrap | female |
| 341 | 3775.0 | 4693.716437 | 4475.927353 | 3839.563668 | 4063.639819 | 4005.109853 | Chinstrap | male |
| 342 | 4100.0 | 4797.866549 | 4449.296758 | 4720.740455 | 4652.013882 | 4803.806832 | Chinstrap | male |
| 343 | 3775.0 | 4745.791493 | 4448.061337 | 4104.268240 | 3672.299099 | 3892.170475 | Chinstrap | female |
333 rows × 8 columns
ECDFs (Funciones acumuladas de probabilidad)
sns.ecdfplot(
data=models_results
)
plt.grid()
plt.show()
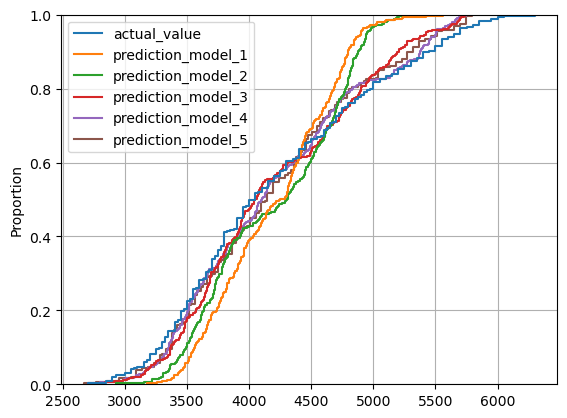
sns.ecdfplot(
data=models_results[['actual_value', 'prediction_model_1', 'prediction_model_5']]
)
plt.grid()
plt.show()
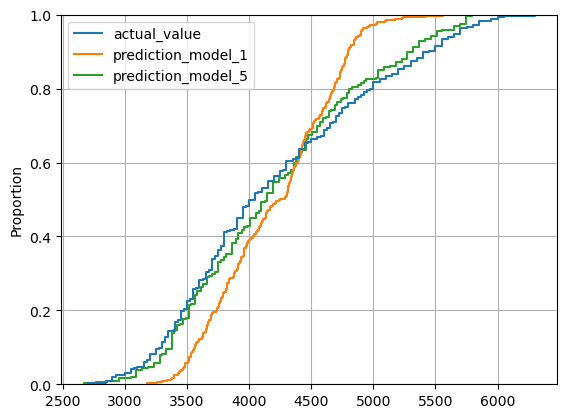
sns.ecdfplot(
data=models_results[['actual_value', 'prediction_model_4']]
)
plt.grid()
plt.show()
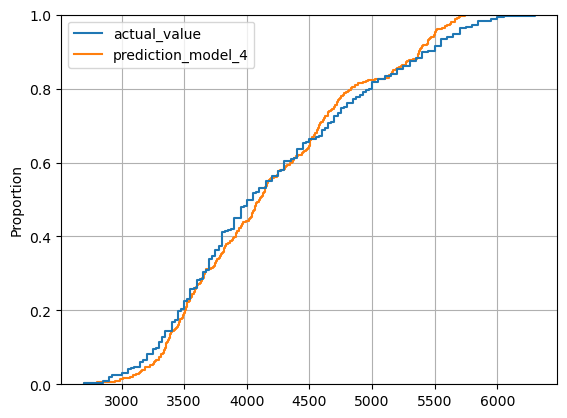
PDFs (Funciones de densidad de probabilidades)
sns.kdeplot(
data=models_results,
cumulative=False # Distribución de probabilidad
)
plt.grid()
plt.show()
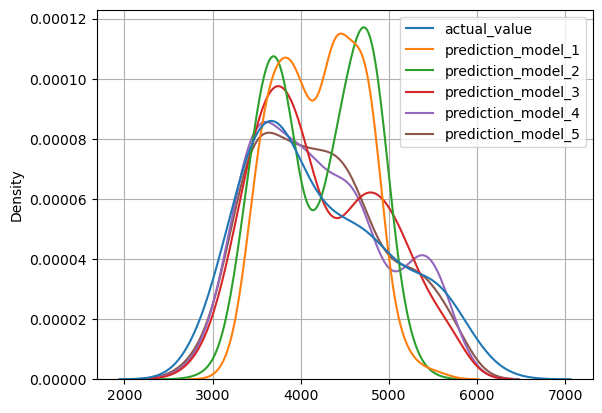
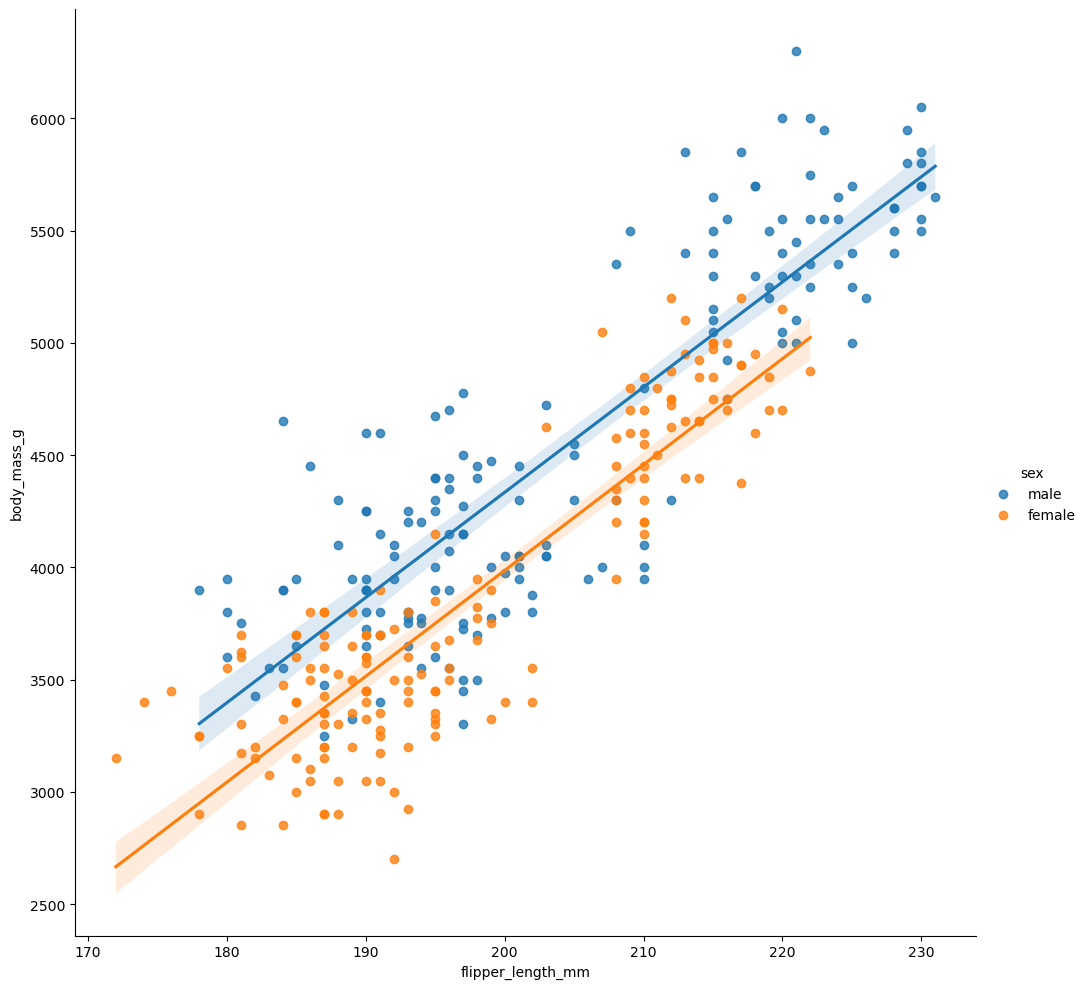
Como recomendación, antes de construir modelos debemos explorar todas las relaciones de variables antes de construir los modelos.
sns.lmplot(
data=processed_penguins_df,
x='flipper_length_mm',
y='body_mass_g',
height=10,
hue='sex'
)
plt.show()
Análisis de regresión logística
Que pasa cuando quiero definir el sexo, esta variables es de tipo categórica.
smf.logit(
formula='numeric_sex ~ flipper_length_mm + bill_length_mm + bill_depth_mm + C(island)',
data=processed_penguins_df
).fit().summary()
Optimization terminated successfully.
Current function value: 0.360900
Iterations 7
| Dep. Variable: | numeric_sex | No. Observations: | 333 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 327 |
| Method: | MLE | Df Model: | 5 |
| Date: | Thu, 19 Dec 2024 | Pseudo R-squ.: | 0.4793 |
| Time: | 19:09:12 | Log-Likelihood: | -120.18 |
| converged: | True | LL-Null: | -230.80 |
| Covariance Type: | nonrobust | LLR p-value: | 8.021e-46 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -61.4464 | 6.944 | -8.849 | 0.000 | -75.057 | -47.836 |
| C(island)[T.Dream] | -1.5596 | 0.493 | -3.163 | 0.002 | -2.526 | -0.593 |
| C(island)[T.Torgersen] | -1.0323 | 0.599 | -1.725 | 0.085 | -2.205 | 0.141 |
| flipper_length_mm | 0.1393 | 0.024 | 5.874 | 0.000 | 0.093 | 0.186 |
| bill_length_mm | 0.1413 | 0.045 | 3.150 | 0.002 | 0.053 | 0.229 |
| bill_depth_mm | 1.6401 | 0.185 | 8.864 | 0.000 | 1.277 | 2.003 |
processed_penguins_df.island.unique()
array(['Torgersen', 'Biscoe', 'Dream'], dtype=object)
Explorando las variables categóricas
(
processed_penguins_df
.value_counts(['island', 'sex', 'species'])
.reset_index(name='count')
)
| island | sex | species | count | |
|---|---|---|---|---|
| 0 | Biscoe | male | Gentoo | 61 |
| 1 | Biscoe | female | Gentoo | 58 |
| 2 | Dream | female | Chinstrap | 34 |
| 3 | Dream | male | Chinstrap | 34 |
| 4 | Dream | male | Adelie | 28 |
| 5 | Dream | female | Adelie | 27 |
| 6 | Torgersen | female | Adelie | 24 |
| 7 | Torgersen | male | Adelie | 23 |
| 8 | Biscoe | female | Adelie | 22 |
| 9 | Biscoe | male | Adelie | 22 |
Podemos definir un modelo que nos ayude a identificar si un pinguino pertenece a determinda especie.
# Seleccionamos solo la especie Adelie
processed_penguins_df = (
processed_penguins_df
.assign(is_adelie=lambda df: df.species.map({'Adelie':1,
'Chinstrap':0,
'Gentoo':0}))
)
model_is_adelie = smf.logit(
formula='is_adelie ~ flipper_length_mm + C(sex)',
data=processed_penguins_df
).fit(maxiter=100)
model_is_adelie.params
Optimization terminated successfully.
Current function value: 0.355225
Iterations 8
Intercept 40.568368
C(sex)[T.male] 1.282656
flipper_length_mm -0.209705
dtype: float64
is_adelie_df_predictions = pd.DataFrame(
dict(
actual_adelie = processed_penguins_df.species.map({'Adelie':1,
'Chinstrap':0,
'Gentoo':0}),
predicted_values = model_is_adelie.predict().round()
)
)
is_adelie_df_predictions
| actual_adelie | predicted_values | |
|---|---|---|
| 0 | 1 | 1.0 |
| 1 | 1 | 1.0 |
| 2 | 1 | 0.0 |
| 4 | 1 | 1.0 |
| 5 | 1 | 1.0 |
| ... | ... | ... |
| 339 | 0 | 0.0 |
| 340 | 0 | 0.0 |
| 341 | 0 | 1.0 |
| 342 | 0 | 0.0 |
| 343 | 0 | 0.0 |
333 rows × 2 columns
En el siguiente código hay cambios respecto al curso.
(
is_adelie_df_predictions
.value_counts(['actual_adelie', 'predicted_values'])
.reset_index(name='count')
.pivot(index='actual_adelie', columns='predicted_values', values='count')
.rename_axis('actual / predicted', axis='index')
.reset_index()
)
| predicted_values | actual / predicted | 0.0 | 1.0 |
|---|---|---|---|
| 0 | 0 | 151 | 36 |
| 1 | 1 | 17 | 129 |
print("Confusion Matrix")
print(
metrics.confusion_matrix(
is_adelie_df_predictions.actual_adelie,
is_adelie_df_predictions.predicted_values
)
)
accuracy = metrics.accuracy_score(
is_adelie_df_predictions.actual_adelie,
is_adelie_df_predictions.predicted_values
)
print(f"Accuracy score: {accuracy:.4f}")
Confusion Matrix
[[151 36]
[ 17 129]]
Accuracy score: 0.8408
Paradoja de Simpson
La paradoja de Simpson es un fenómeno en análisis de datos donde una tendencia que aparece en varios grupos de datos desaparece o se invierte cuando se combinan esos grupos.
Características Clave:
- Grupos: Los datos están divididos en subgrupos que muestran una tendencia específica.
- Combinación: Al agrupar todos los datos, la tendencia puede cambiar, lo que puede llevar a conclusiones erróneas.
- Ejemplo: En un estudio sobre el rendimiento de estudiantes, un grupo puede mostrar que los estudiantes de una disciplina tienen mejores calificaciones, pero al combinar con otra disciplina, la tendencia se invierte.
La paradoja de Simpson resalta la importancia de considerar la segmentación de los datos y cómo la agregación puede ocultar patrones significativos.
sns.regplot(
data=processed_penguins_df,
x='bill_length_mm',
y='bill_depth_mm'
)
plt.show()
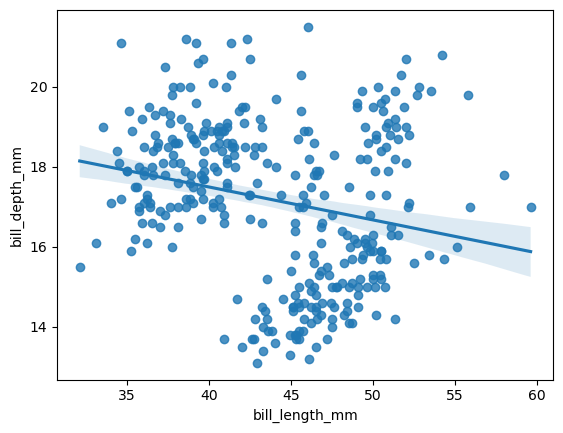
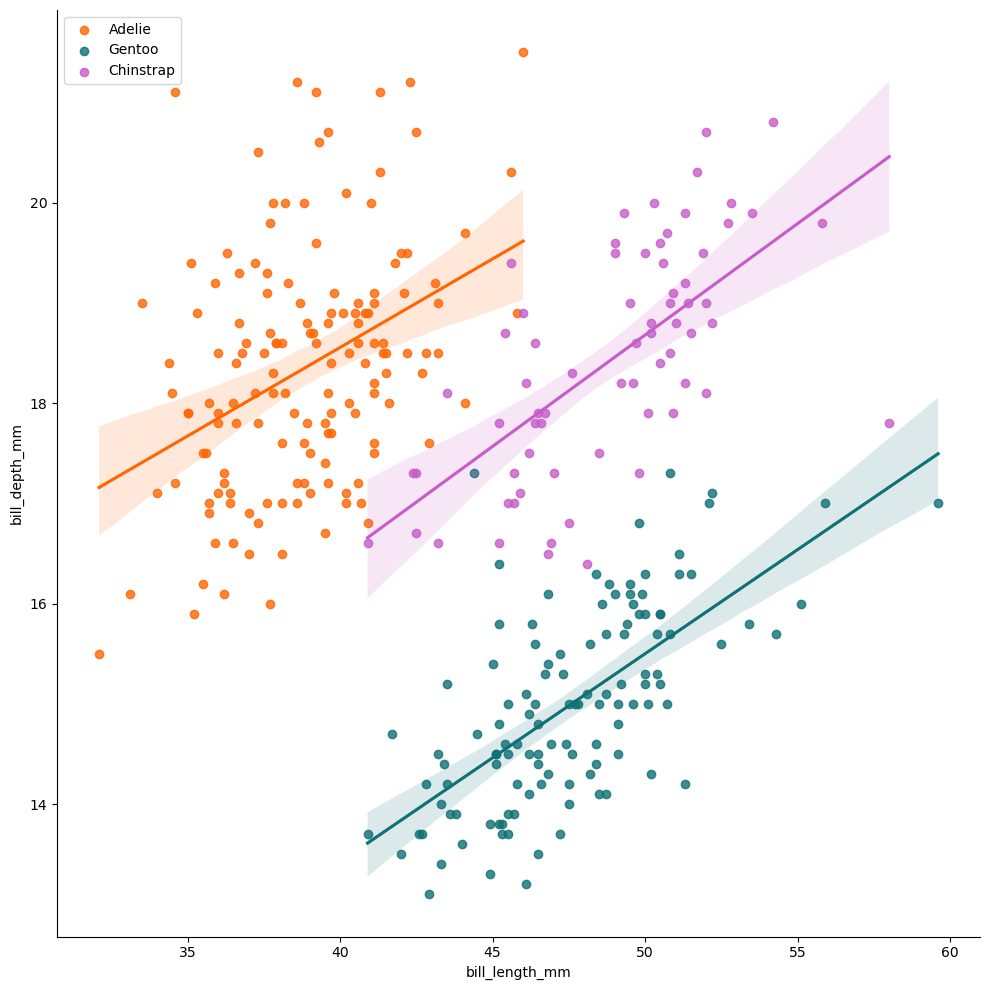
Si observamos acá vemos que la relación entre la longitud del pico y la altura del pico es negativa, es decir si una disminuye la otra también. Pero si agregamos el tipo de especie en la relación anterior podemos observar una dinámica totalmente diferente.
sns.lmplot(
data=processed_penguins_df,
x='bill_length_mm',
y='bill_depth_mm',
hue='species',
height=10,
palette=penguin_color,
legend=False
)
plt.legend()
plt.show()
sns.pairplot(data=processed_penguins_df,
hue='species',
palette=penguin_color)
plt.show()
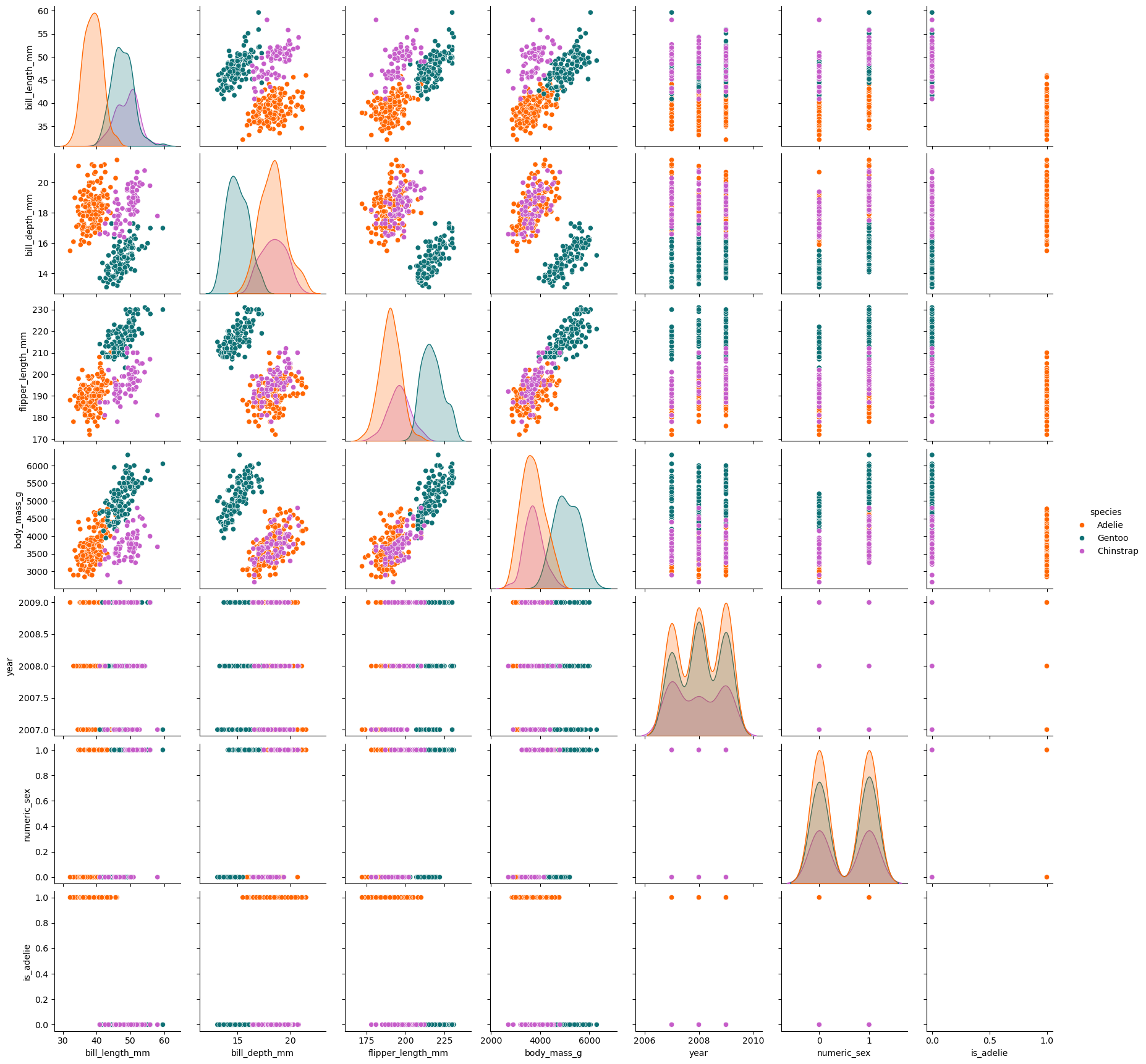
¿Qué hacer cuando tengo muchas variables?
Cuando se trabaja con muchas variables, el análisis par a par puede volverse confuso. Por ello, es necesario utilizar técnicas que simplifiquen la comprensión de la variación en los datos al reducir las dimensiones, permitiendo así visualizar todo en un único espacio (por ejemplo, transformar 10 variables en solo 2). Algunas de estas técnicas incluyen:
- Análisis de Componentes Principales (PCA): Un uso práctico de esta técnica es demostrar cómo los genes están relacionados con la geografía de Europa.
- TSNE (T-Distributed Stochastic Neighbor Embedding): Se utiliza para diferenciar entre los diversos tipos de cáncer.
- UMAP (Uniform Manifold Approximation and Projection for Dimension Reduction): Esta técnica busca preservar la estructura local de los datos mientras captura la estructura global a través de proyecciones en un plano.
- Comparación: Se refiere a la evaluación del rendimiento de un algoritmo de reducción de dimensiones frente a un conjunto de datos específico.
Diversidad de gráficas al explorar datos
Si bien existen reglas que te ayudarán a encontrar el gráfico apropiado para tu problema, tu imaginación debe estar siempre abierta a crear e iterar sobre el aspecto y comunicación de los gráficos.
Los estadísticos y las gráficas son solo un par de herramientas, pero la exploración de datos va más allá y se fundamenta en la resolución de preguntas.
Resumiendo
Las preguntas son la fuente de toda exploración. Asegúrate de definir qué quieres encontrar y quién necesita consultar los resultados desde un comienzo. Es fundamental identificar el tipo de análisis de datos y variables que se requieren. Explora las dimensiones de tu conjunto de datos y qué tipos de variables contiene. Siempre visualiza los estadísticos. Todos los conjuntos de datos son diferentes, conócelos más allá de sus números de resumen. Visualiza una o varias variables de distintas maneras. La diversidad de gráficas te permitirá conocer a detalles los matices de los datos.
Atención
Este tutorial es basado en el Curso de Análisis Exploratorio de Datos de Platzi.