Matemáticas para Data Science: Estadística Descriptiva
Published:
Tutorial introductorio a la estadística descriptiva para ciencias de datos.
Intro
Entendemos por estadística descriptiva, de forma sencilla, la tarea de resumir los datos para obtener información. Por otra parte, la estadísticca inferencial nos permite predecir información a partir de los datos.
¿Puede mentir con estadística? Uno puede equivocarse debido a que no hay una definición objetiva. Los diferentes estadísticos descriptivos dan nociones diferentes sobre los mismos datos.
Sugerencia de Libro: Naked Statistics, Charles Wheelan.
¿Porque aprender estadística?
- Resumir grandes cantidades de información.
- Tomar mejores o peores decisiones.
- Responder preguntas con relevancia social.
- Reconocer patrones en los datos.
- Descubrir a quienes usan estas herramientas con fines nefastos.
Flujo de trabajo en Data Science
- Tipos de datos, pipeline de procesamiento:
- Ingesta de datos
- Validación
- Análisis exploratorio, estadística descriptiva, correlaciones, reducciones de datos:
- Preparación
- Entrenamiento modelo
- Probabilidad e inferencia
- Evaluación modelo
- Test de hipótesis:
- Modelo en producción
- Interacción usuario final
Estadísticos para ingesta y procesamiento.
Estadísticos para analítica y exploración.
Tipos de datos
- Categóricos (género, categoría de película, método de pago):
- ordinal (
object,bool) (Ordinales: Relación de orden.) - nominal
- ordinal (
- Numéricos (edad, altura, temperatura):
- discreto
int64 - continuo
float64
- discreto
Uso de
describe()para generar un conjunto completo de estadísticos descriptivos.
Medidas de tendencia central
- Media (promedio): es susceptible a valores atípicos. \(\bar{x}=\frac{1}{N}\sum_{i=1}^{N} x_i\)
- Mediana (dato central): necesidad de ordenar el conjunto de datos. \(\text{median}(x) = \left\{\begin{array}{cl} \frac{x[N/2]+x[N/2 + 1]}{2} & : \ N~\text{par} \\ \frac{N+1}{2} & : \ N~\text{impar} \end{array}\right.\)
- Moda (dato que más se repite): no aplica para datos numéricos continuos.
Medidas de dispersión
- Rango: \((\max - \min)\)
- Rango intercuartil: Distancia entre Q1 y Q3. Definido por los cuartiles deben ser homogéneos, es decir la misma cantidad de datos.
- Desviación estándar: \(\sigma=\sqrt{\frac{1}{N}\sum_{i=1}^N (x_i - \mu)^2}.\) La varianza es \(\sigma^2= \frac{1}{N}\sum_{i=1}^N (x_i - \mu)^2.\)
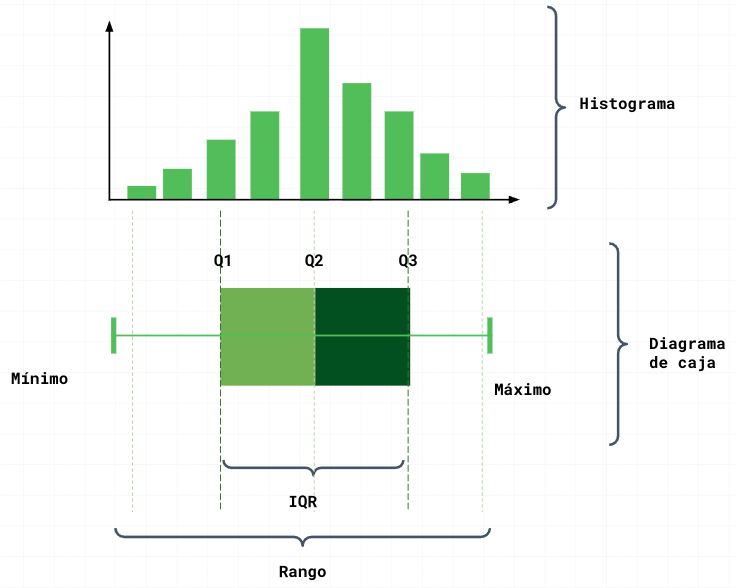
- Q2: Parte a la mitad, es la mediana.
- Q1: la mitad entre la mediana y el mínimo.
- Q3: la mitad entre la mediana y el máxima.
Nota de color: Podemos tener desviación estándar de la muestra de un población: \(\sigma_{\text{sample}}=\sqrt{\frac{1}{N}\sum_{i=1}^N (x_i - \mu)^2}\)
Analicemos una distribución normal:
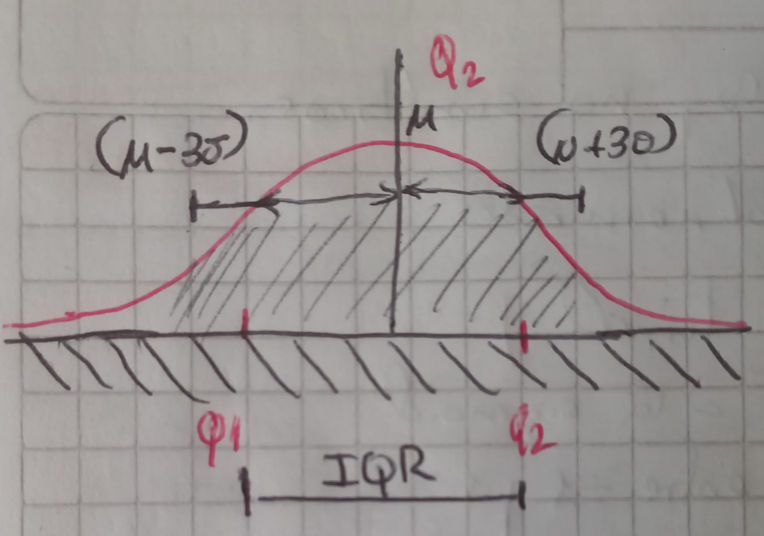
Percentiles son un caso particular de los cuantiles.
Dentro de \((\mu - 3\sigma; \mu + 3\sigma)\) está el 99.72% de los datos.
Para detectar datos outliers tomamos los datos fuero de este rango \(\left\{\begin{array}{cl} \text{Q1} - 1.5~\text{IQR} & \to \min \\ \text{Q1} + 1.5~\text{IQR} & \to \max \end{array}\right.\)
Si la distribución es sesgada 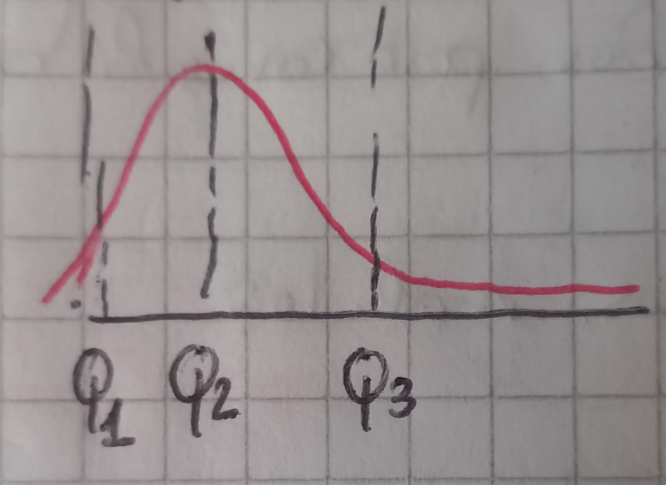
Aplicamos el siguiente criterio generalizado: \(\left\{\begin{array}{cl} \text{Q1} - 1.5~\text{f(IQR)} & \to \min \\ \text{Q1} + 1.5~\text{f(IQR)} & \to \max \end{array}\right.\) donde f(IQR) es una función definida dependiente del IQR.
Trabajar con cuartiles es mejor para distribuciones no simétricas para detectar outliers.
Exploración visual de los datos
Se puede encontrar en Datavizproject, una ayuda para explorar que tipo de imagen visual puede ayudar a mostrar la información resumida.
Recordar que se puede realizar una análisi univariado, bivariado o multivariado.
Histograma de datos
Q7_df = df[(df['manufacturer_name']=='Audi') & (df['model_name']=='Q7')]
sns.histplot(Q7_df, x='price_usd', hue = 'year_produced')
Diagrama de dispersión (Análisis bivariado)
Scatterplot: visualizamos las muestra de los datos. **Parámetrohueimportante para separar por datos específicos.sns.displot(df, x="price_usd", hue="engine_type")-> Código Python.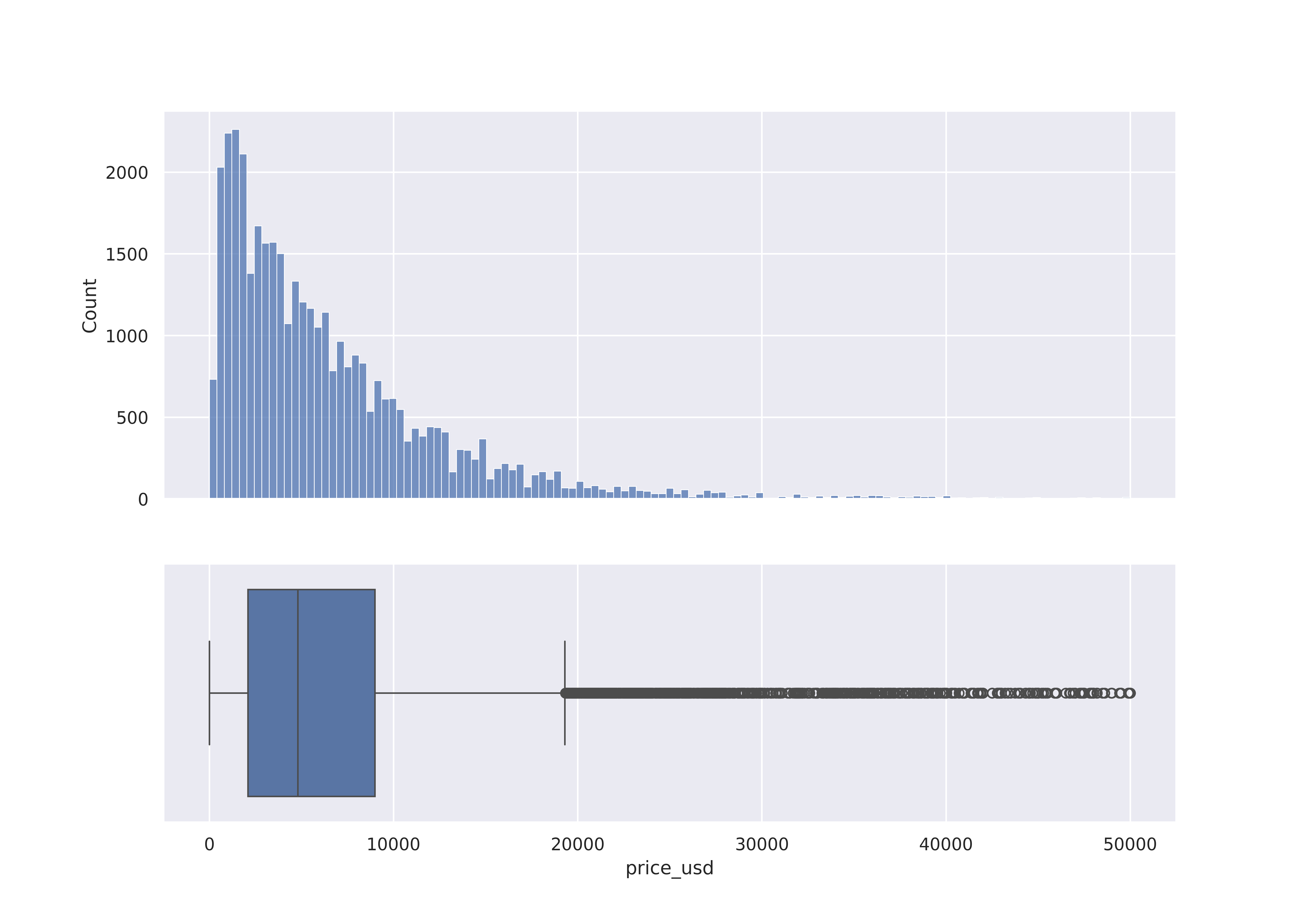
Jointplot: ajusta los datos a una curva para ver una suave curva de distribución.sns.jointplot(data=iris, x = 'sepal_length', y = 'petal_length', hue = 'species')-> Código Python.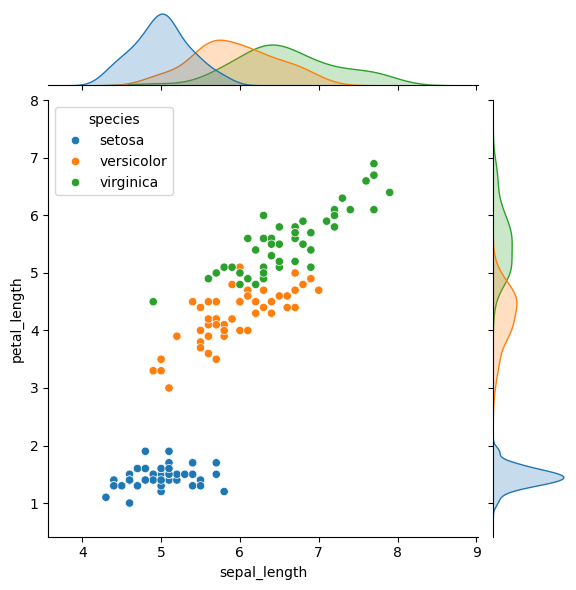
Pipelines de procesamiento de datos numéricos
El escalamiento lineal es importante debido a que los modelos de machine learning eficientes en el rango [-1, 1]. Existen diferentes tipos: max-min, Clipping, Z-score, Winsorizing, etc. Debemos emplear el escalamiento lineal cuando la data simétrica o uniformemente distribuida.
max-min: aplicar la siguiente transformación \(x_s = \frac{2x-\min-\max}{\max-\min}\)Clipping: sacamos los datos fuera del rango, y los colapsamos al valor de los rangos. Esta nos una buena alternativa de procesamiento de los datos porque incluso los datos outliers son importantes para el modelo.Winsorizing: es un caso particular declipping.Z-score: aplicar la siguiente transformación: \(z = \frac{x_i - \mu}{\sigma}\)
Las transformaciones no lineales son necesarias para datos fuertemente sesgados, no simétricos. Existen diferentes tipos: Logaritmos, sigmoides, polinomiales, etc. Es necesario emplearlas antes de escalamientos lineales.
La cantidad transformaciones sobre distribuciones sesgadas oara convertirlas en no sesgadas es infinito.
Ejemplo de transformación no lineal \(y = \tanh(x_i).\) Estas es una buena transformación no lineal, pues a la salida tenemos datos cuasi homogéneos.
Notas de aplicación en Python
timeitMedir performance de los modelos.
Observamos que:
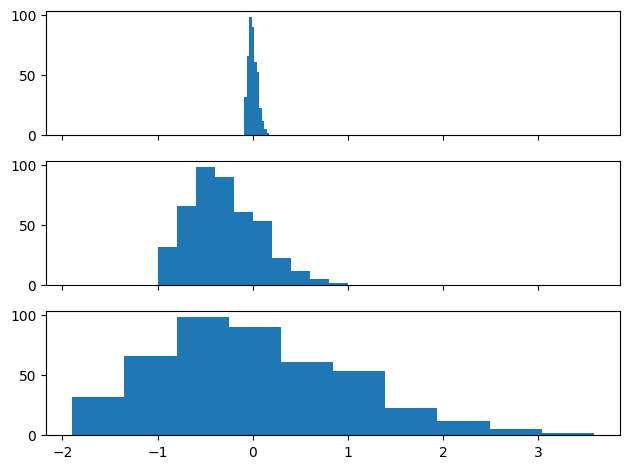
max-min: mejor para datos uniformemente distribuidos.Z-score: mejor para datos distribuidos normalmente. (Gaussiana)
El
apply()en Pandas se aplica sobre columnas empleando funciones lambdas.
Scikit-learn: Tiene toda una parte para preprocesamiento.
# escalamiento max-min
max_raw = max(raw)
min_raw = min(raw)
scaled = (2*raw - max_raw -min_raw)/(max_raw - min_raw)
# normalización Z-score
avg = np.average(raw)
std = np.std(raw)
z_scaled = (raw - avg)/std
fig, axs = plt.subplots(3, 1, sharex=True, tight_layout=True)
axs[0].hist(raw)
axs[1].hist(scaled)
axs[2].hist(z_scaled)
plt.show()
Pipelines de procesamiento de datos categóricos
Mapeos numéricos:
- Dummy:
- Representación compacta.
- Mejor para inputs linealmente independientes.
- One-hot:
- Permite describir categorías no incluidas inicialmente.
Ambas estrategias permiten mapear numéricamente las categorías.
En Pandas tenemos la función get_dummies, pasa al tipo True o False. (pd.get_dummies('data'))
Mientras en scikit-learn se tiene la función OneHotEncoder.
import sklearn.preprocessing as preprocessing
encoder = preprocessing.OneHotEncoder(handle_unknown='ignore')
| Categoría | Dummy | One_hot |
|---|---|---|
| English | [0, 0] | [1, 0, 0] |
| Spanish | [0, 1] | [0, 1, 0] |
| French | [1, 0] | [0, 0, 1] |
La diferencia radica que para la función OneHotEncoder al aparecer un valor nuevo desconocido lo codifica como [0, 0, 0]. Mientras que la función dummy lo omite.
Correlaciones
En los scatterplot se puede observar como un dato variaba respecto a otro dato.
Si hay variables correlacionadas, no aportan información por tanto algunas de ellas pueden ser eliminadas.
Obtengamos la covarianza \(\frac{1}{N-1}\sum_{i=1}^N (x_i - \mu_x)(y_i - \mu_y)\)
A partir de la covarianza podemos obtener el coficiente de correlación: \(\rho = \frac{\text{cov}}{\sigma_x \cdot \sigma_y}\)
Tenemos los siguientes casos:
- Para un coeficiente correlación cercano a 0, indica que no existe correlación.
- Para un coeficiente correlación cercano a 1, indica una alta correlación.
- Para un coeficiente correlación cercano a -1, indica una alta correlación inversa. Es decir, si una variable aumenta la otra disminuye.
Es importante destacar que la correlación no implica causalidad. Es decir, si dos variables están fuertemente correlacionadas, esto no implica que una es causa de otra. (Puede que una variable este ligada causalmente con otra, pero la correlación no es una prueba suficiente.)
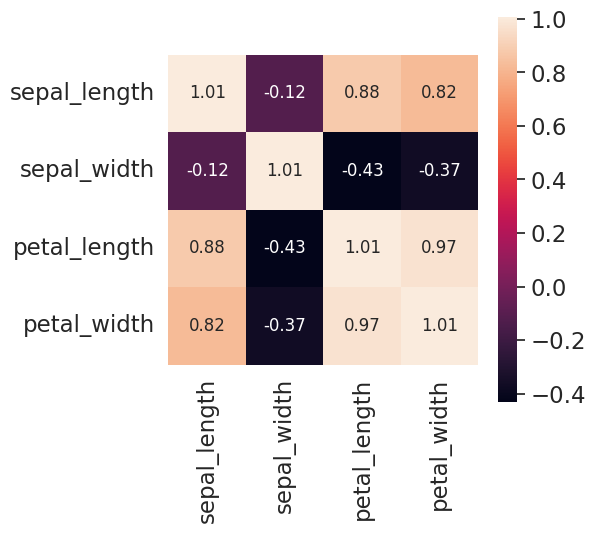
Matriz de covarianza
La matriz de covarianza muestra la relación a través de la covarianza empleando la correlación entra variables. Con pocas vairables es una buena opción.
plt.figure(figsize=(5,5))
sns.set(font_scale=1.5)
hm = sns.heatmap(covariance_matrix,
cbar=True,
annot=True,
square=True,
fmt='.2f',
annot_kws={'size': 12},
yticklabels=['sepal_length', 'sepal_width', 'petal_length', 'petal_width'],
xticklabels=['sepal_length', 'sepal_width', 'petal_length', 'petal_width'])
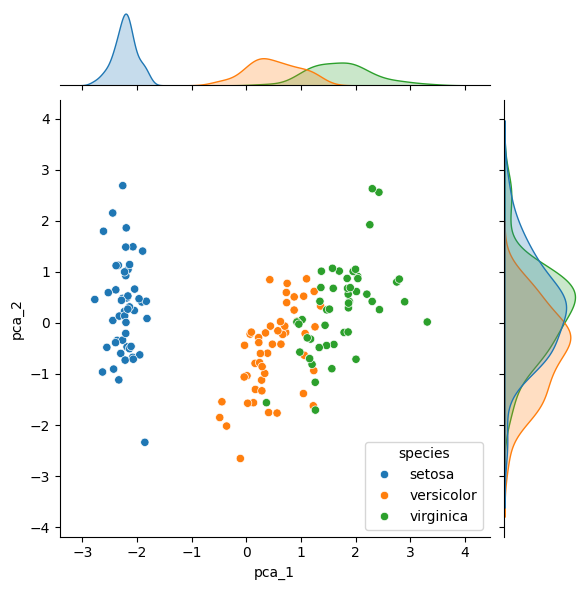
Análisis de PCA
Capturar la dimensión de mayor varianza y proyectar sobre esta los datos. Esto lo hacemos de descomponer la matriz de covarianza en vectores y valores propios y la dirección con máxima dispersión la empleamos como vector de proyección.
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(scaled)
reduced_scaled = pca.transform(scaled)
iris['pca_1'] = reduced_scaled[:,0]
iris['pca_2'] = reduced_scaled[:,1]
sns.jointplot(x=iris['pca_1'], y=iris['pca_2'], hue = iris['species'])
Proyección de vectores
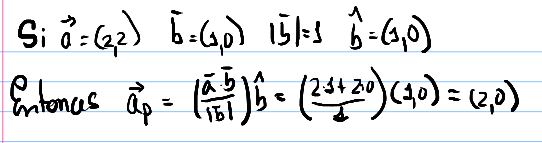
Vectores y Valores propios de una matriz
En álgebra lineal podemos tener ecuaciones donde la incógnita es un vector, supongamos la siguiente ecuación: \(A \cdot \vec{x} = \lambda \vec{x}\)
Aquí A es una matriz cuadrada NxN cuyos elementos conocemos perfectamente y X es un vector columna cuyas componentes desconocemos. Aquí recordemos que multiplicar un vector por un número es simplemente multiplicar cada componente del vector por dicho número.
import numpy as np
A = np.array([[1, 2], [1, 0]])
values, vectors = np.linalg.eig(A)
El comando np.linalg.eig(A) lo que hace es calcular directamente los valores y vectores propios, llamados values y vectors en el código, respectivamente. Verás que esta matriz tiene dos valores propios:
array([ 2., -1.])
Con sus respectivos vectores propios asociados:
array([[ 0.89442719, -0.70710678 ],
[ 0.4472136 , 0.70710678 ]])
Aquí es importante anotar que los vectores que entrega la función np.linalg.eig(A) son vectores columna de manera que los elementos de la primera columna de vectors corresponden con el primer valor de values y así sucesivamente.
Puedes verificar que cada vector y su respectivo valor propio cumplen la ecuación original ejecutando cada parte así:
np.matmul(A, vectors.T[1])
Que te da como resultado:
array([ 0.70710678, -0.70710678])
Mientras que por otro lado calculando:
values[1]*vectors.T[1]
Resulta en lo mismo:
array([ 0.70710678, -0.70710678])
Uno de los hechos más importantes de obtener los vectores y valores propios de una matriz es poder diagonalizarla. En general se define que una matriz A es diagonalizable si es posible escribirla como el producto de: \(A = P \cdot D \cdot P^{-1}\) Donde D es una matriz diagonal (matriz donde todos los elementos por fuera de la diagonal son cero).
Y aquí un resultado matemático bien conocido es que si una matriz es diagonalizable, la matriz D se construye colocando sus valores propios en la diagonal y la matriz P se construye colocando en cada columna el vector propio,siguiendo el mismo orden de valores propios correspondientes de la matriz D, así:
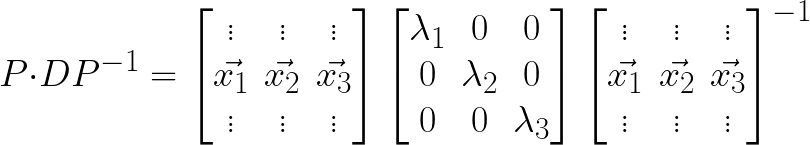
Cuando aplicamos este cálculo de vectores y valores propios a una matriz de covarianza, los vectores representan las direcciones a lo largo de las cuales percibimos la mayor cantidad de varianza de ese conjunto de datos, donde la cantidad de varianza es proporcional al valor propio de cada vector propio. Y es importante tener en cuenta que este procedimiento aplica para un conjunto de datos con N variables al que le corresponde una matriz de covarianza de tamaño NxN.
Ahora, el último factor importante de esta técnica es que para matrices de covarianza, sus vectores propios siempre son independientes unos de otros y esto es justamente lo que queremos en un proceso de reducción de variables, porque direcciones independientes implica que estos vectores representan nuevas variables cuya correlación es la más baja posible y así cada nueva variable es lo más representativa posible.
En álgebra lineal se dice más precisamente que los vectores propios de una matriz de covarianza son ortogonales y esto quiere decir que el producto interno de cualquier par de estos vectores siempre da como resultado cero: \(\vec{x_i} \cdot \vec{x_j} = 0\)
Como consecuencia la matriz se denomina matriz ortogonal, y se sabe en matemáticas que la inversa de una matriz ortogonal es igual a la transpuesta, de manera que:
\[A = P \cdot D \cdot P^{-1} = P \cdot D \cdot P^{T}\]Atención
Este tutorial es basado en el Curso de Matemáticas para Data Science: Estadística Descriptiva de Platzi.