Funciones Matemáticas para Data Science e Inteligencia Artificial
Published:
Curso Funciones Matemáticas para Data Science e Inteligencia Artificial de PLATZI
Funciones Matemáticas para Data Science e Inteligencia Artificial

Elemental
Las funciones nos permiten modelar nuestra realidad.
Podemos entender una función como una máquina donde entra un elemento \(x\) y sale un elemento \(y\).
En el caso de una variable \(y = f(x)\), donde \(y\) es la variable dependiente y \(x\) la variable independiente.
Una función es una regla donde cada elemento de un conjunto A se le asigna un elemento de un conjunto B.
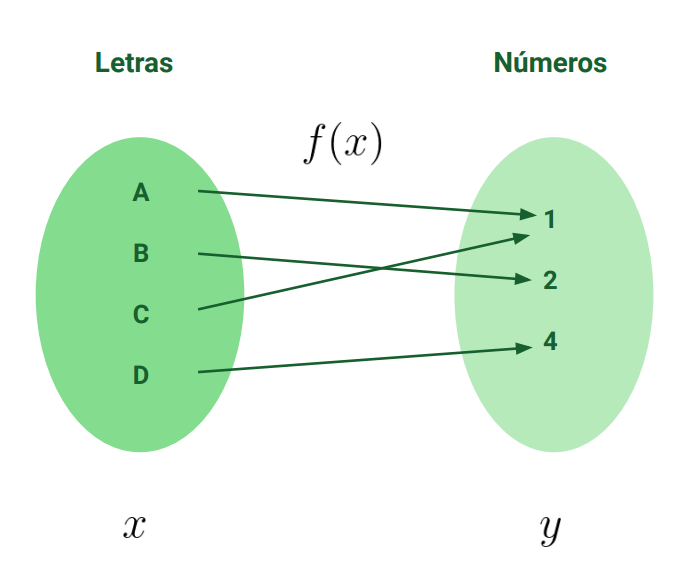
Formas de representar una función
- Verbalmente
- Numéricamente
- Visualmente
- Algebraicamente
Tipos de variables
- Variables cualitativas:
- Nominales: Son a las que les asignamos una cualidad. Por ejemplo; los colores de un LED pueden ser rojo, verde o azul.
- Ordinales: Como su nombre lo dice, representan un orden. La altura de un objeto se puede clasificar como alto, medio o bajo.
- Binarias: Solo toman dos valores, usualmente usadas para representar estados. Existe o no existe, está frío o caliente, uno o cero, son algunos ejemplos.
- Variables cuantitativas:
- Discretas: Son finitas y toman ciertos valores, como los números en una tabla por ejemplo. Pueden verse como variables separadas por un “paso”. Por ejemplo, una persona puede tener 0, 1, 2 o 3 amigos pero nunca 3.5.
- Continuas: Sus valores pueden verse como infinitos al tomar cualquier valor dentro de los números reales en un rango establecido. Por ejemplo: Medir la estatura de una persona.
Dominio y rango de una función
¿Qué valores pueden tener las funciones?: Los valores que toma \(x\) y que están definidos en la función \(f(x)\). Esto es lo que conocemos como dominio.
Por otra parte, el rango de una función son todos los resultados que nos puede dar una función.
Cómo leer matemáticas: Símbolos generales
Debemos tener conocimiento sobre los símbolos de igualdad y relación (\(=, \gt, \lt, \approx, \dots\)), de operaciones acumulativas (\(\sum_{n=0}^3 n, \prod_{n=0}^3 n, \dots\)).
Símbolos matemáticos generales más usados
Cómo leer matemáticas: Conjuntos
Conjuntos los podemos identificar como círculos. A los cuales podemos aplicar operaciones como unión, intersección, pertenencia, y otras.
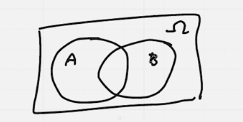
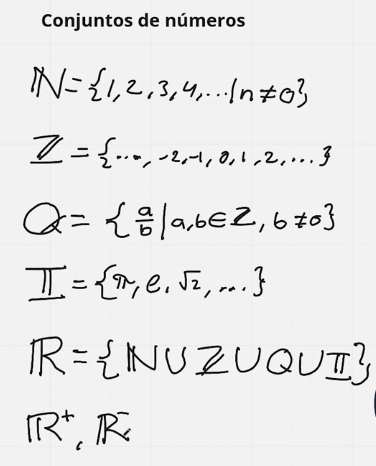
Función/Aplicación
Lo siguiente \(f: \mathbb{X} \to \mathbb{Y}\) significa que existe una función que nos lleva del conjunto \(\mathbb{X}\) al conjunto \(\mathbb{Y}\). De forma parecida tenemos una función \(f: \mathbb{R} \to \mathbb{R}^+\), es decir que nos lleva de los números reales a los números reales positivos. (Función absoluta)
Todo sobre funciones
Funciones algebraicas lineales
Tiene la forma de \(f(x)=mx + b\) donde \(m\) y \(b\) \(\in R\). \(m\) puede ser calculada por: \(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
y \(b\) es el punto de corte con el eje \(y\). Su dominio es \(Dom_{f} = (-\infty, \infty)\). Su imagen es \(Im_{f} = (-\infty, \infty)\)
N = 100
m = -1
b = 3
def f(x):
return m*x+b
x = np.linspace(-10,10, num=N)
y = f(x)
fig, ax = plt.subplots()
ax.plot(x,y)
ax.grid()
plt.show()
Nota: Decimos que es decreciente si \(m\) es negativa, y creciente si \(m\) es positiva. Siempre el valor \(b\) es donde la función corta al eje y.
Funciones algebraicas polinómicas
Funciones polinómicas
Tiene la forma de \(P(x)=a_{n}x^{n} + a_{n-1}x^{n-1}+...+a_{2}x^{2}+a_{1}x + a_{1}\)
a una función que tiene esta forma se le llama polinomio de grado \(n\). A los elementos \(a\) los llamaremos coeficientes donde \(a \in R\).
Por ejemplo:
\[P(x)= 2x^{7} - x^{4} + 3x^{2} + 4\]que es un polinomio de grado 7.
def f(x):
return (2*x**7)-(x**4)+(3*x**2)+4
x = np.linspace(-10,10, num=N)
y = f(x)
plt.plot(x, y)
plt.grid()
plt.show()
Funciones potencia
Hay unas funciones que son un caso particular de las funciones polinómicas que son las funciones potencia, las cuales tienen la forma:
\[f(x)= x^{a}, a \in R\]Por ejemplo:
\[f(x)= x^{2}\]El dominio de \(f(x)=x^{2}\) es \(Dom_{f} = (-\infty, \infty)\). Su imagen es \(Im_{f} = [0, \infty)\)
def f(x):
return x**7
y = f(x)
plt.plot(x,y)
plt.grid()
plt.show()
Funciones trascendentes
Son funciones que no pueden ser expresadas con polinomios.
Funciones trigonométricas
Algunos ejemplos son las funciones \(\cos(x)\), \(\sin(x)\) y \(\tan(x)\).
def f(x):
return np.cos(x)
y = f(x)
plt.plot(x,y)
plt.show()
Función exponencial
Tienen la forma de \(f(x)=a^x\) donde la base \(a\) es una constante positiva. Un gran ejemplo de una función exponencial es usando la base como el número de euler:
\[f(x)=e^x\]def f(x):
return np.exp(x)
y=f(x)
plt.plot(x,y)
plt.show()
Función logaritmo
El logaritmo está definido por la relación: \(log_{b}(x) = n \Longleftrightarrow x=b^n\) donde:
- la \(b\) es la base.
- la \(n\) es el exponente al que está elevado la base.
- la \(x\) es el resultado de elevar la base \(b\) al exponente \(n\).
Ejemplo:
Teniendo b=2 y n=8, entonces:
\[2^8=256\]Por lo que \(x=256\). Calculando el logaritmo base 2 de \(x\) es:
\[log_{2}(256) = 8\]def f(x):
return np.log2(x)
x = np.linspace(0.001,256, num=1000)
plt.plot(x,f(x))
plt.show()
Funciones seccionadas
Son funciones que tienen diferentes valores definidos por un intervalo. Por ejemplo la función escalón de Heaviside:
\[H(x) = \begin{cases} 0, &\quad \text{para, } x < 0 \\ 1, &\quad\text{para. } x \ge 0 \\ \end{cases}\]def H(x):
Y = np.zeros(len(x))
for idx,x in enumerate(x):
if x>=0:
Y[idx]=1
return Y
N=1000
x = np.linspace(-10,10, num=N)
y = H(x)
plt.plot(x,y)
plt.show()
Funciones compuestas
Definición: Conocidas las funciones \(f\) y \(g\), la composición de \(f\) y \(g\) está dada por: \(\begin{aligned} f\circ g=(f\circ g)(x)=f(g(x)) \end{aligned}\)
import numpy as np
import matplotlib.pyplot as plt
N = 1000
x = np.linspace(-10,10, num=N)
def g(x):
return x**2
def f(x):
return np.sin(x)
y = g(x)
f_o_g = f(g(x))
plt.plot(x,f_o_g)
plt.show()
¿Cómo manipular funciones?
Desplazamientos verticales y horizontales
Siendo \(c\) una constante mayor que cero, entonces la gráfica:
- empleando \(y=f(x)+c\) se desplaza \(c\) unidades hacia arriba.
- empleando \(y=f(x)-c\) se desplaza \(c\) unidades hacia abajo.
- empleando \(y=f(x-c)\) se desplaza \(c\) unidades hacia la derecha.
- empleando \(y=f(x+c)\) se desplaza \(c\) unidades hacia la izquierda.
N = 1000
def f(x):
return x**2;
c = 4
x = np.linspace(-10,10, num=N)
y = f(x + c)
fig, ax = plt.subplots()
ax.plot(x,y)
ax.grid()
ax.axhline(y=0, color='r')
ax.axvline(x=0, color='r')
plt.show()
Alargamientos y compresiones
Siendo \(c\) una constante mayor que cero, entonces la gráfica:
- en \(y=c \cdot f(x)\) alarga la gráfica verticalmente en un factor de \(c\).
- en \(y= \frac{1}{c} \cdot f(x)\) comprime la gráfica verticalmente en un factor de \(c\).
- en \(y=f(c \cdot x)\) comprime la gráfica horizontelmente en un factor de \(c\).
- en \(y= f(\frac{1}{c} \cdot x )\) alarga la gráfica horizontelmente en un factor de \(c\).
N = 1000
def f(x):
return np.sin(x);
c = 2
x = np.linspace(-15,15, num=N)
y = f((1/c)*x)
fig, ax = plt.subplots()
ax.plot(x,y)
ax.grid()
ax.axhline(y=0, color='r')
ax.axvline(x=0, color='r')
plt.show()
Reflexiones
- en este caso \(y=-f(x)\) refleja la gráfica respecto al eje x.
- en este caso \(y=f(-x)\) refleja la gráfica respecto al eje y.
N = 1000
def f(x):
return x**3;
x = np.linspace(-10,10, num=N)
y = f(-x)
fig, ax = plt.subplots()
ax.plot(x,y)
ax.grid()
ax.axhline(y=0, color='r')
ax.axvline(x=0, color='r')
plt.show()
Características de las funciones
Función par
Una función es par si cumple la siguiente relación a lo largo de su dominio: \(f(-x) = f(x)\). Si lo notaste, esta relación nos dice que una función es par si es simétrica al eje vertical (eje Y). Por ejemplo, una parábola es una función es par.
Función impar
Una función es impar si cumple la siguiente relación a lo largo de su dominio: \(f(-x) = -f(x)\). Esta relación nos indica que una función es impar si es simétrica al eje horizontal (eje X). Por ejemplo, una función cúbica es impar.
Función acotada
Una función es acotada si su codominio (también conocido como rango o imagen) se encuentra entre dos valores, es decir, está acotado. Esta definición se define como que hay un número m que para todo valor del dominio de la función se cumple que: \(-m \le f(x) \le m\). or ejemplo, la función seno o coseno están acotadas en el intervalo [-1, 1] dentro de su co-dominio.
Funciones periódicas
Las funciones periódicas son aquellas que se repiten cada cierto periodo, este periodo se denomina con la letra T. La relación que debe cumplir la función para ser periódica es la siguiente. \(f(x) = f(x + T), T \neq 0\). Por ejemplo, la función seno y coseno son funciones periódicas con un periodo \(T = 2\pi\). Es decir que si nosotros calculamos \(f(x)\) y calculamos \(f(x + 2\pi)\) en la función seno el valor que nos den ambas expresiones es el mismo.
En ciencia de datos
Una lectura introductoria sería a través de wikipedia, te comparto el enlace: https://es.wikipedia.org/wiki/Neurona.
THE PERCEPTRON: A PROBABILISTIC MODEL FOR INFORMATION STORAGE AND ORGANIZATION IN THE BRAIN
Neurona Artificial
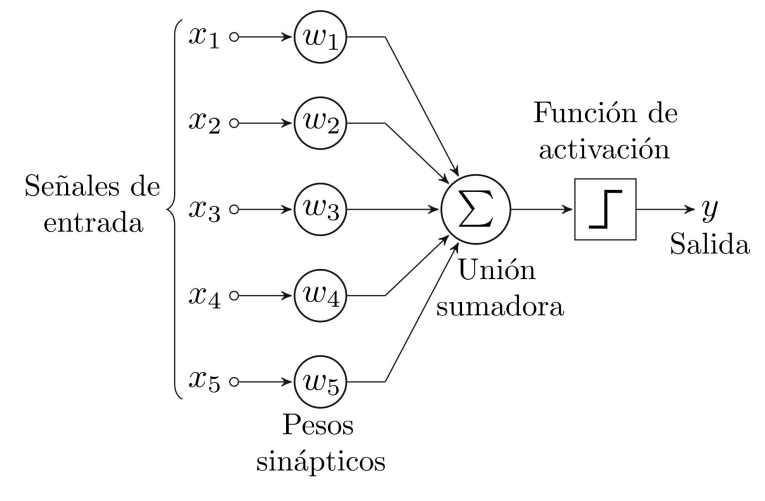
Funciones de activación
Función lineal
def f(x):
return x
plt.plot(x, f(x))
plt.grid()
plt.show()
Función escalón o de Heaviside
\(H(x) = \begin{cases} 0, &\quad \text{para, } x < 0 \\ 1, &\quad\text{para. } x \ge 0 \\ \end{cases}\)
def H(x):
Y = np.zeros(len(x))
for idx,x in enumerate(x):
if x>=0:
Y[idx]=1
return Y
N=1000
y = H(x)
plt.plot(x,y)
plt.grid()
plt.show()
Función sigmoide
Es una de las funciones de activación más empleadas, su empleo en la regresión logística es fundamental. \(f(x)=\frac{1}{1-e^{-x}}\). Su rango siempre esta en 0 y 1, por lo que este acotamiento tiene mucho uso.
def f(x):
return 1/(1 + np.exp(-x))
N=1000
y = f(x)
plt.plot(x,y)
plt.grid()
plt.show()
Función tangente hiperbólica
Es una función de escalamiento, y presenta un problema en el algoritmo de backpropagation. \(f(x)=\frac{2}{1+e^{-2x}}-1\)
def f(x):
return np.tanh(x)
N=1000
y = f(x)
plt.plot(x,y)
plt.grid()
plt.show()
Función ReLU
Esta función es la reina de las funciones de activación en el Deep Learning, su derivada es fácil de obtener, por tanto su empleo en el algoritmo de backpropagattion es sencillo.
\[R(x)=max(0,x)\]def f(x):
return np.maximum(x,0)
N=1000
y = f(x)
plt.plot(x,y)
plt.grid()
plt.show()
Modelado
Entendiendo la regresión lineal simple
La regresión lineal simple es un modelo estadístico que analiza la relación entre dos variables:
- Variable independiente (X): Es la variable que se supone explica o predice el comportamiento de otra.
- Variable dependiente (Y): Es la que queremos predecir o entender.
El modelo ajusta una línea recta a los datos según la ecuación: \(Y = b_0 + b_1X + \epsilon\)
- donde \(b_0\) es la intersección o término constante (donde la línea cruza el eje Y),
- donde \(b_1\) es la pendiente, que indica el cambio en \(Y\) por cada unidad de cambio en \(X\),
- y \(\epsilon\) representa los errores o las desviaciones de los datos reales respecto a la línea ajustada.
Se usa para predecir valores de \(Y\) a partir de valores de \(X\) o para entender la relación lineal entre ambas variables. El ajuste se realiza minimizando la suma de los errores al cuadrado (método de mínimos cuadrados).
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Datos de ejemplo
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1) # Horas estudiadas (Variable independiente)
Y = np.array([2, 4, 5, 4, 5]) # Calificación obtenida (Variable dependiente)
# Crear el modelo de regresión lineal
modelo = LinearRegression()
# Ajustar el modelo
modelo.fit(X, Y)
# Predicciones
Y_pred = modelo.predict(X)
# Parámetros del modelo
print(f"Intersección (b0): {modelo.intercept_}")
print(f"Pendiente (b1): {modelo.coef_[0]}")
# Visualizar los resultados
plt.scatter(X, Y, color='blue', label='Datos reales') # Datos reales
plt.plot(X, Y_pred, color='red', label='Línea de regresión') # Línea ajustada
plt.xlabel('Horas estudiadas')
plt.ylabel('Calificación obtenida')
plt.legend()
plt.show()
¿Cómo se calcula un error? ¿Cómo se calcula un error?
El error lo obtenemos como \(\text{e} = \hat{y} - {y}\), donde \(\hat{y}\) es la predicción. Para obtener el error preferimos calcular al cuádrado con el objetivo de buscar el mínimo quede una función cóncava y fácil de derivar, entonces \(\text{e}^2 = (\hat{y} - {y})^2\). Ahora si analizamos para todos los puntos podemos obtener el error cuadrático medio \(\mathbf{ECM} = \sum_{i=1}^N (\hat{y} - {y})^2.\)